| sexo_factor | Media | Mediana | Desv. Estándar |
|---|---|---|---|
| Hombre | 2.86 | 2.10 | 2.68 |
| Mujer | 4.96 | 4.11 | 3.90 |
Introducción al Análisis Bivariado y Tipos de Asociación
Unidad 5: Estadística Descriptiva Bivariada
2025-11-10
Objetivos de la Sesión de Hoy
- Definir el análisis bivariado y la distinción entre variable explicativa (X) y variable respuesta (Y).
- Clasificar los tres tipos de relaciones bivariadas según el nivel de medición de las variables.
- Introducir el concepto estadístico de independencia como punto de referencia para evaluar asociaciones.
- Asociar cada tipo de relación con su herramienta de análisis numérico y visual principal.
1. De Describir a Relacionar
El Salto al Análisis Bivariado
Hasta ahora, en la Unidad 4, nos hemos enfocado en el análisis univariado: describir cada variable por separado (su forma, centro y dispersión).
Sin embargo, el corazón del análisis sociológico reside en entender relaciones.
- ¿Cómo se relaciona la educación con el ingreso?
- ¿El género afecta la carga de trabajo doméstico?
- ¿La zona de residencia se asocia con la percepción de seguridad?
Hoy comenzamos el análisis bivariado: el estudio de la relación entre dos variables a la vez.
Variable Explicativa y Variable Respuesta
En el análisis bivariado, asignamos roles a nuestras variables para estructurar nuestra pregunta de investigación.
- Variable Explicativa (o Independiente, X):
- Es la variable que creemos que influye, explica o predice un cambio en la otra.
- En un modelo causal, es la “causa”.
- Variable Respuesta (o Dependiente, Y):
- Es la variable que mide el resultado o el fenómeno que queremos explicar.
- En un modelo causal, es el “efecto”.
Ejemplo: En la pregunta “¿Cómo afecta el sexo (X) a la cantidad de horas de trabajo no remunerado (Y)?”, el sexo es la variable explicativa y las horas de trabajo son la variable respuesta.
Convención: Al graficar, la variable explicativa (X) siempre va en el eje horizontal y la variable respuesta (Y) en el eje vertical.
El Problema Sociológico del Uso del Tiempo
El tiempo es un recurso universal, pero su distribución y uso no lo son. Es un recurso escaso que se reparte de manera desigual según ejes clave de la estructura social como el sexo, el nivel socioeconómico o el territorio.
Gran parte del trabajo que sostiene a la sociedad, como las tareas domésticas y de cuidados, es trabajo no remunerado, históricamente invisibilizado y feminizado.
La Encuesta Nacional de Uso del Tiempo (ENUT) es la principal herramienta en Chile para medir este fenómeno. Su objetivo es cuantificar cómo las personas distribuyen su tiempo entre el trabajo remunerado, el trabajo no remunerado y las actividades personales, haciendo visible lo invisible para el diseño de políticas públicas más equitativas.
2. La Caja de Herramientas del Análisis Bivariado
Tres Tipos de Relaciones
La forma en que analizamos una relación bivariada depende fundamentalmente del tipo de variables que estemos cruzando (categóricas o cuantitativas).
Esto nos da tres casos principales, cada uno con su propio set de herramientas:
- Categórica (X) ➞ Cuantitativa (Y)
- Categórica (X) ➞ Categórica (Y)
- Cuantitativa (X) ➞ Cuantitativa (Y)
Caso 1: Categórica (X) ➞ Cuantitativa (Y)
- Pregunta Clave: ¿Existen diferencias en el promedio (o la distribución) de una variable cuantitativa entre distintos grupos?
- Ejemplo: ¿Dedican hombres y mujeres, en promedio, la misma cantidad de tiempo al trabajo doméstico no remunerado (
t_tnr_dt)? - ¿El ingreso promedio (
Y) difiere entre hombres y mujeres (X)? - ¿Los años de escolaridad (
Y) varían según la región de residencia (X)?
- Ejemplo: ¿Dedican hombres y mujeres, en promedio, la misma cantidad de tiempo al trabajo doméstico no remunerado (
- Herramienta de Análisis Numérico:
- Comparación de estadísticos descriptivos por grupo (medias, medianas, desviaciones estándar, etc.)
- Herramienta de Análisis Visual:
- Boxplots comparativos o gráficos de densidad por grupo.
Caso 1: Tabla de Estadísticos por Grupo
Analizamos las horas diarias de trabajo no remunerado (t_tnr_dt) por sexo.
La tabla revela una marcada brecha de género. En promedio, las mujeres dedican 4.96 horas diarias al trabajo no remunerado, casi 2.1 horas más que los hombres (2.86 horas). La mediana confirma esta tendencia: el 50% de las mujeres dedica 4.11 horas o más, mientras que el 50% de los hombres dedica 2.10 horas o más. Además, la mayor desviación estándar en las mujeres (3.90) sugiere que existe más variabilidad en sus cargas de trabajo no remunerado que entre los hombres.
Caso 1: Gráfico de Boxplots Comparativos
La visualización confirma la brecha observada en la tabla.
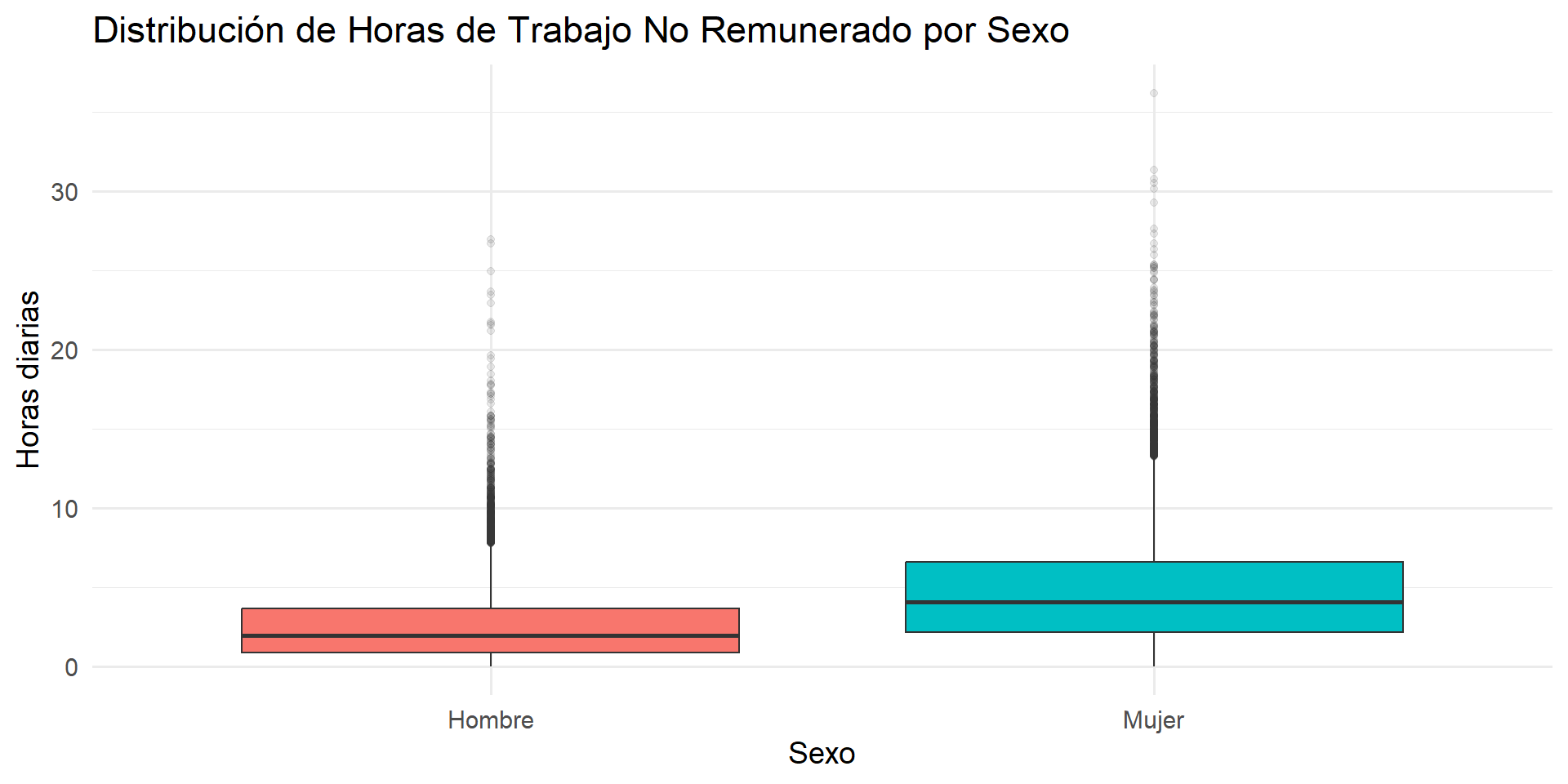
La visualización confirma la magnitud de la brecha. El boxplot de las mujeres está completamente por encima del de los hombres, indicando una diferencia estructural. La mediana de las mujeres (la línea central de su caja) es superior al tercer cuartil de los hombres (el borde superior de su caja). Esto implica que más del 50% de las mujeres dedica más tiempo al trabajo no remunerado que el 75% de los hombres.
Caso 1: Gráfico de Densidad Comparativo
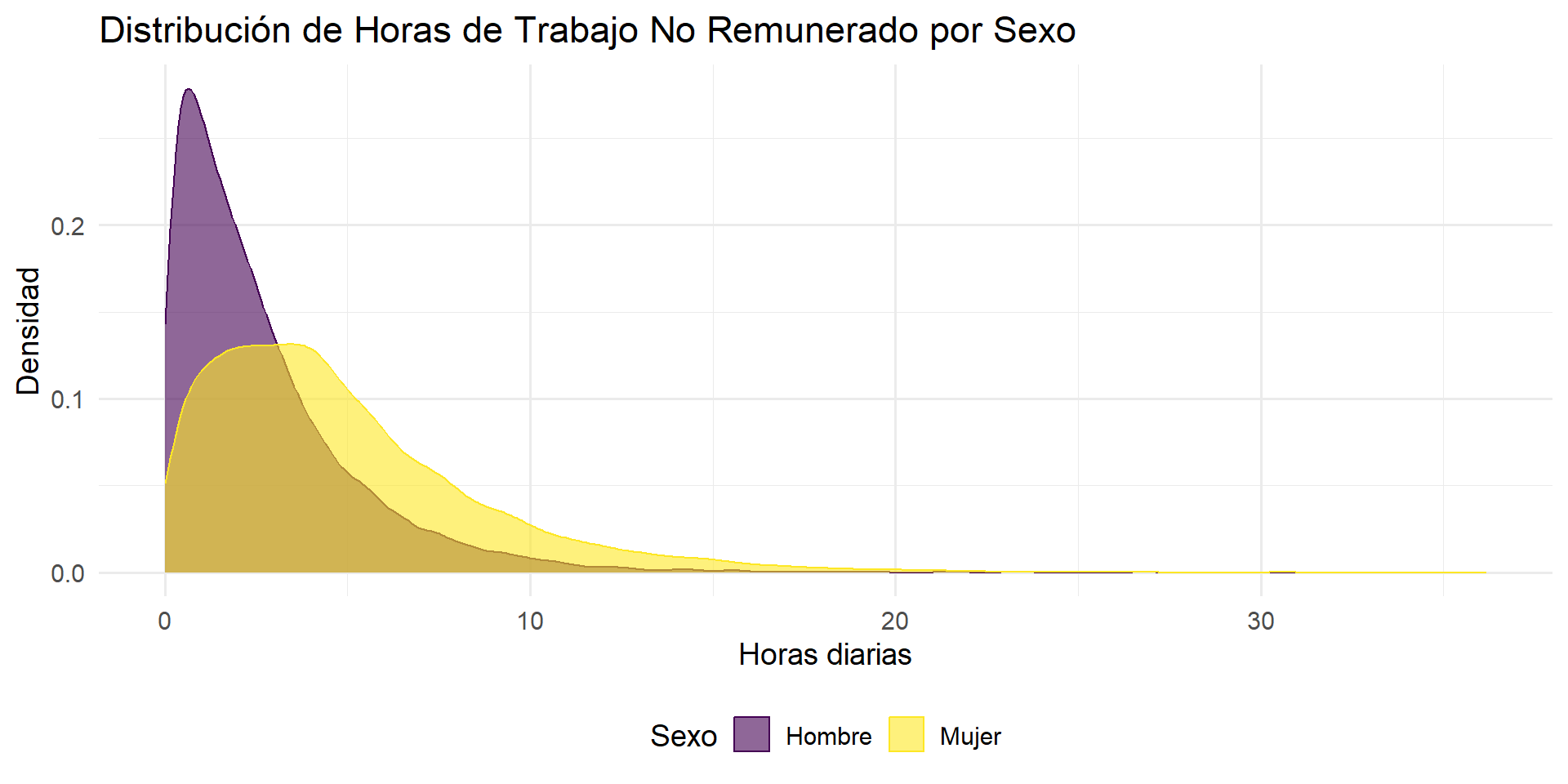
Caso 2: Categórica (X) ➞ Categórica (Y)
Pregunta Clave: ¿La probabilidad de pertenecer a una categoría de Y depende de la categoría de X a la que se pertenece?
- Ejemplo: ¿La satisfacción con el reparto de tareas domésticas (
bs2) se relaciona con el sexo de la persona? - ¿La situación de pobreza (
Y) se asocia con el nivel educacional (X)? - ¿La afiliación política (
Y) varía según el grupo religioso (X)?
- Ejemplo: ¿La satisfacción con el reparto de tareas domésticas (
Herramienta de Análisis Numérico:
- Tablas de contingencia (tablas cruzadas) con porcentajes condicionales.
Herramienta de Análisis Visual:
- Gráficos de barras apiladas.
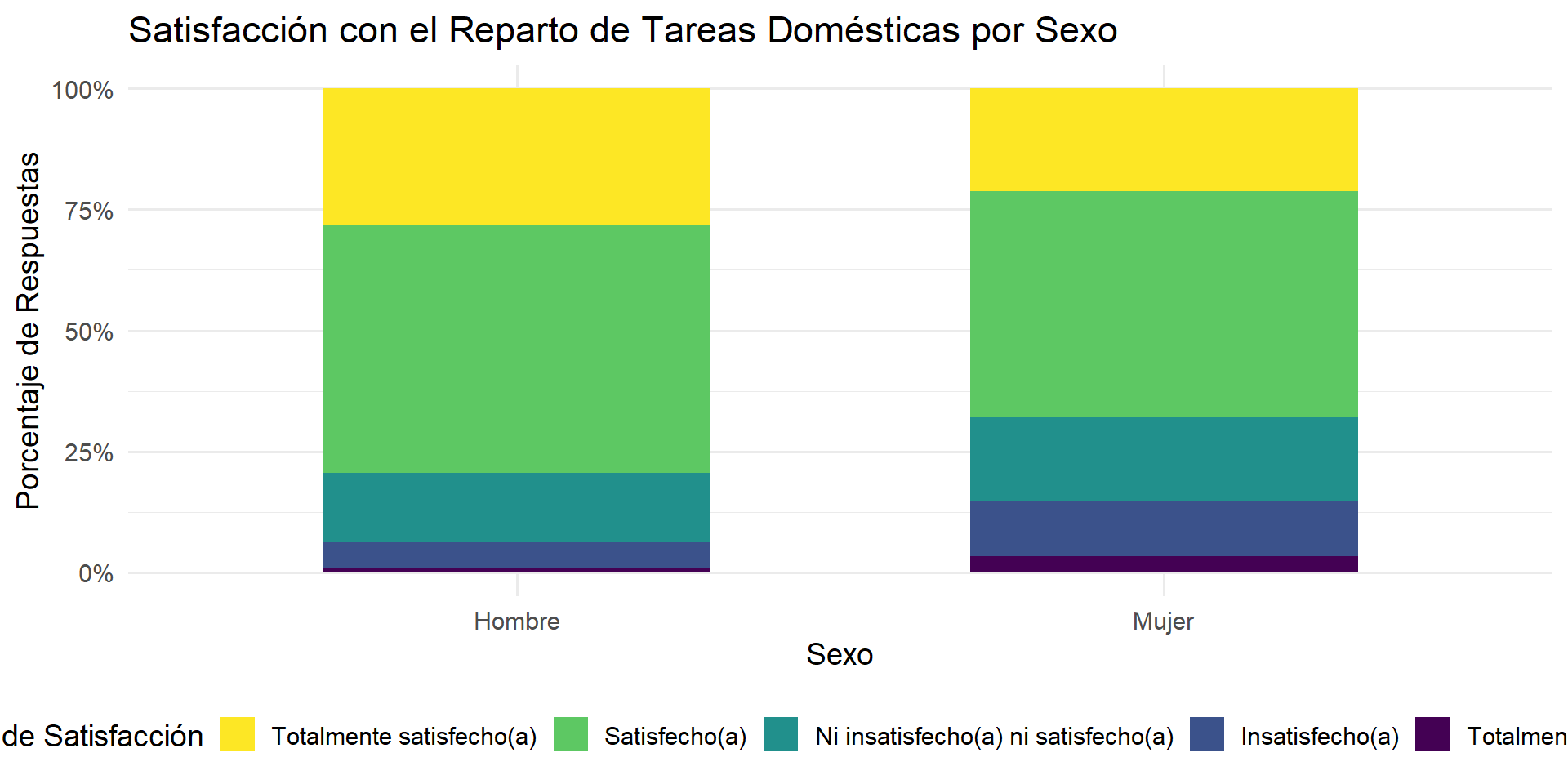
Caso 2: Tabla de Contingencia
Analizamos la relación entre sexo (X) y atisfacción con el reparto de tareas domésticas (Y).
| bs2_factor | Hombre | Mujer |
|---|---|---|
| Totalmente insatisfecho(a) | 1.0 | 3.3 |
| Insatisfecho(a) | 5.2 | 11.5 |
| Ni insatisfecho(a) ni satisfecho(a) | 14.2 | 17.3 |
| Satisfecho(a) | 51.2 | 46.7 |
| Totalmente satisfecho(a) | 28.3 | 21.2 |
La tabla muestra que un porcentaje mayor de hombres (28.3%) que de mujeres (21.2%) siente que está “Totalmente satisfecho(a)” con el reparto de tareas. Inversamente, las mujeres reportan más insatisfacción (14.8% sumando “Insatisfecha” y “Totalmente Insatisfecha”, vs. 6.2% en hombres).
Caso 2: Gráfico de Barras Apiladas al 100%
Este gráfico visualiza los porcentajes de la tabla anterior.
Caso 3: Cuantitativa (X) ➞ Cuantitativa (Y)
- Pregunta Clave: A medida que X aumenta, ¿Y tiende a aumentar, disminuir o no cambia?
- Ejemplo: A mayor
edad(X), ¿cómo cambia el tiempo dedicado al trabajo doméstico no remunerado (t_tnr_dt, Y)? - A mayor edad (
X), ¿mayor o menor ingreso (Y)? - A más años de escolaridad (
X), ¿mayor prestigio ocupacional (Y)?
- Ejemplo: A mayor
- Herramienta de Análisis Numérico:
- Coeficiente de correlación.
- Herramienta de Análisis Visual:
- Gráfico de dispersión (Scatterplot).
Caso 3: Tabla de Correlación
Calculamos la correlación de Pearson entre edad y trabajo no remunerado total para cuantificar su relación lineal. El coeficiente varía entre −1 y 1: 1 indica asociación lineal positiva perfecta, −1 indica asociación lineal negativa perfecta y 0 indica ausencia de asociación lineal (aunque puede existir una relación no lineal).
| Correlacion |
|---|
| 0.104 |
El coeficiente de correlación de Pearson es de 0.104. Al ser un valor positivo pero muy cercano a cero, indica que existe una asociación lineal muy débil entre la edad y las horas de trabajo no remunerado. Si solo miráramos este número, concluiríamos que la edad no es un factor relevante para predecir la carga de trabajo doméstico.
Caso 3: Gráfico de Dispersión
El gráfico de dispersión nos cuenta una historia más compleja.
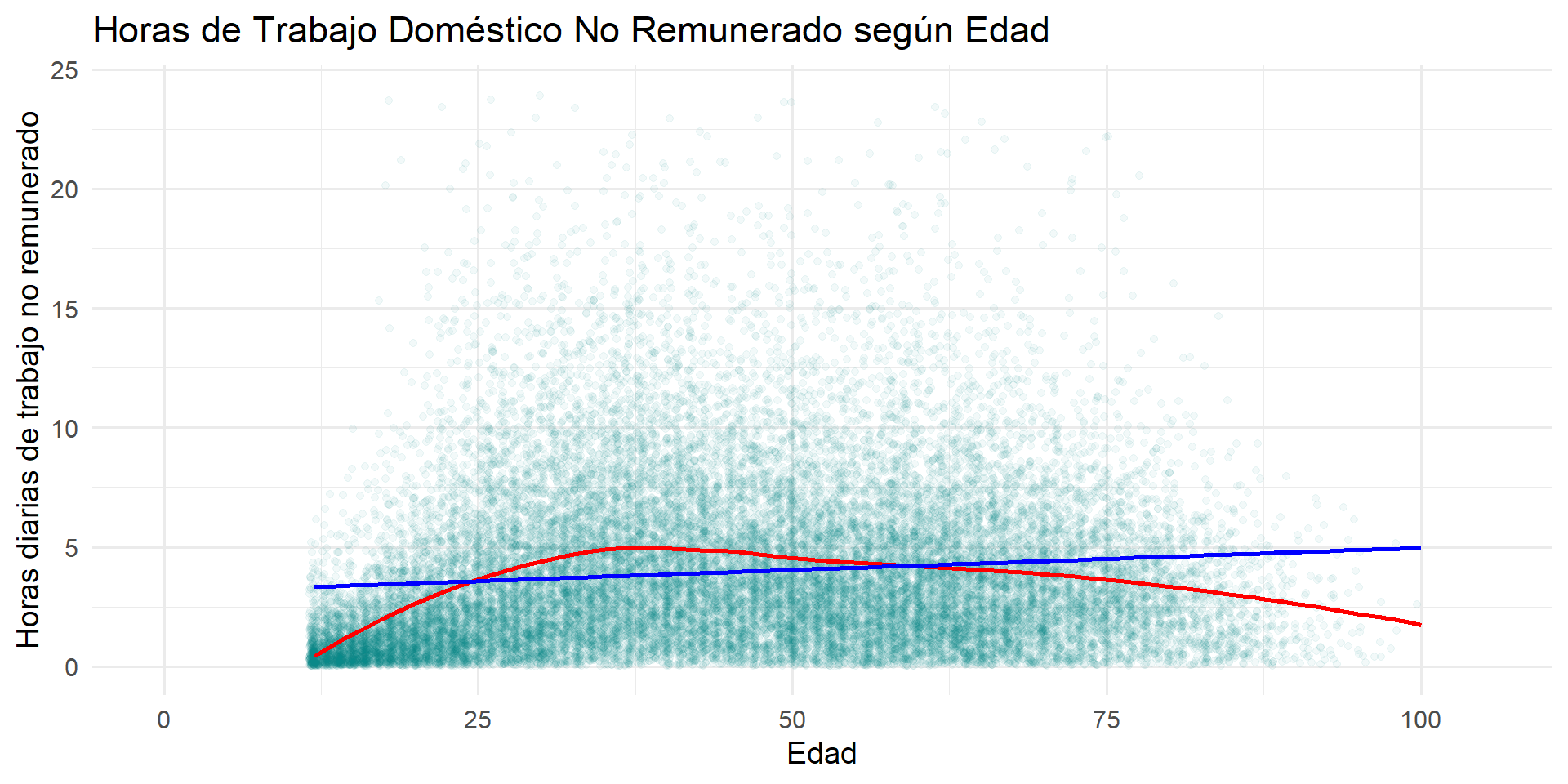
La relación entre edad y trabajo no remunerado no es lineal, sino curvilínea, con forma de U invertida. La carga de trabajo no remunerado tiende a aumentar desde la juventud, alcanza su punto máximo en la adultez media (aproximadamente entre los 40 y 50 años, coincidiendo con la crianza y consolidación del hogar) y luego disminuye gradualmente en la vejez.
El Punto de Referencia: Independencia Estadística
Antes de poder decir que dos variables están “relacionadas”, necesitamos un punto de referencia.
Definición de Independencia: Dos variables son estadísticamente independientes si conocer el valor de una no nos da ninguna información sobre el valor probable de la otra.
El Objetivo del Análisis Bivariado: Nuestro trabajo como analistas es buscar evidencia en contra de la independencia. Buscamos patrones sistemáticos que demuestren que las variables sí están relacionadas.
- En nuestros tres ejemplos, encontramos evidencia clara de que las variables no son independientes.
Cierre y Próximos Pasos
Resumen de la sesión de hoy:
- El análisis bivariado estudia la relación entre una variable explicativa (X) y una respuesta (Y).
- Existen tres casos principales de análisis bivariado, cada uno con sus propias herramientas visuales y numéricas.
- El concepto de independencia es nuestro punto de partida: buscamos evidencia de que las variables están, de hecho, asociadas.
En el práctico de hoy:
- Aplicarán estas herramientas en R para explorar los tres tipos de relaciones utilizando la ENUT 2023.
Adelanto de la próxima clase:
- Nos sumergiremos en el Caso 2 (Categórica ➞ Categórica). Aprenderemos a construir e interpretar tablas de contingencia y a introducir una tercera variable de control.
