Visualizando Distribuciones y Medidas Robustas
Unidad 4: Estadística Descriptiva Univariada
2025-10-20
Objetivos de la Sesión de Hoy
- Introducir el marco para describir una variable cuantitativa: Forma, Centro y Dispersión.
- Aprender a visualizar la forma de una distribución usando Histogramas.
- Calcular e interpretar las medidas de centro y dispersión robustas: Mediana, Cuartiles y Rango Intercuartil (IQR).
- Construir e interpretar el Resumen de Cinco Números y su visualización: el Boxplot.
1. Descripción de Variables Cuantitativas
De las Categorías a los Números
En la clase anterior, aprendimos a describir variables categóricas contando casos y mostrando porcentajes (table, count, geom_bar).
Hoy, pasamos a las variables cuantitativas (de intervalo o razón), como la edad, los ingresos o los años de escolaridad.
Con estas variables, un simple conteo no es suficiente. Necesitamos herramientas para describir su distribución: cómo se reparten los valores a lo largo de un rango numérico.
Análisis Exploratorio de Datos
Al enfrentarnos a una variable cuantitativa, nuestro objetivo es describir tres características fundamentales de su distribución:
- Forma: ¿Cuál es el aspecto general de la distribución? ¿Es simétrica o asimétrica? ¿Tiene uno o varios picos (modas)?
- Centro: ¿Alrededor de qué valor se agrupan los datos? ¿Cuál es el “caso típico”?
- Dispersión (o Variabilidad): ¿Qué tan extendidos o concentrados están los datos?
Además, siempre debemos estar atentos a la presencia de valores atípicos (outliers), que son observaciones que se desvían marcadamente del patrón general.
2. Visualizando la Forma: Histogramas
El Histograma: Un Retrato de la Distribución
El histograma es la principal herramienta gráfica para visualizar la forma de la distribución de una variable cuantitativa.
- ¿Cómo se construye?
- El rango de la variable se divide en intervalos de igual ancho, llamados “bins” o “clases”.
- Se cuenta cuántas observaciones caen dentro de cada intervalo.
- Se dibuja una barra para cada intervalo, donde la altura de la barra es proporcional a la frecuencia.
A diferencia de un gráfico de barras, en un histograma el eje X es continuo y las barras van juntas.
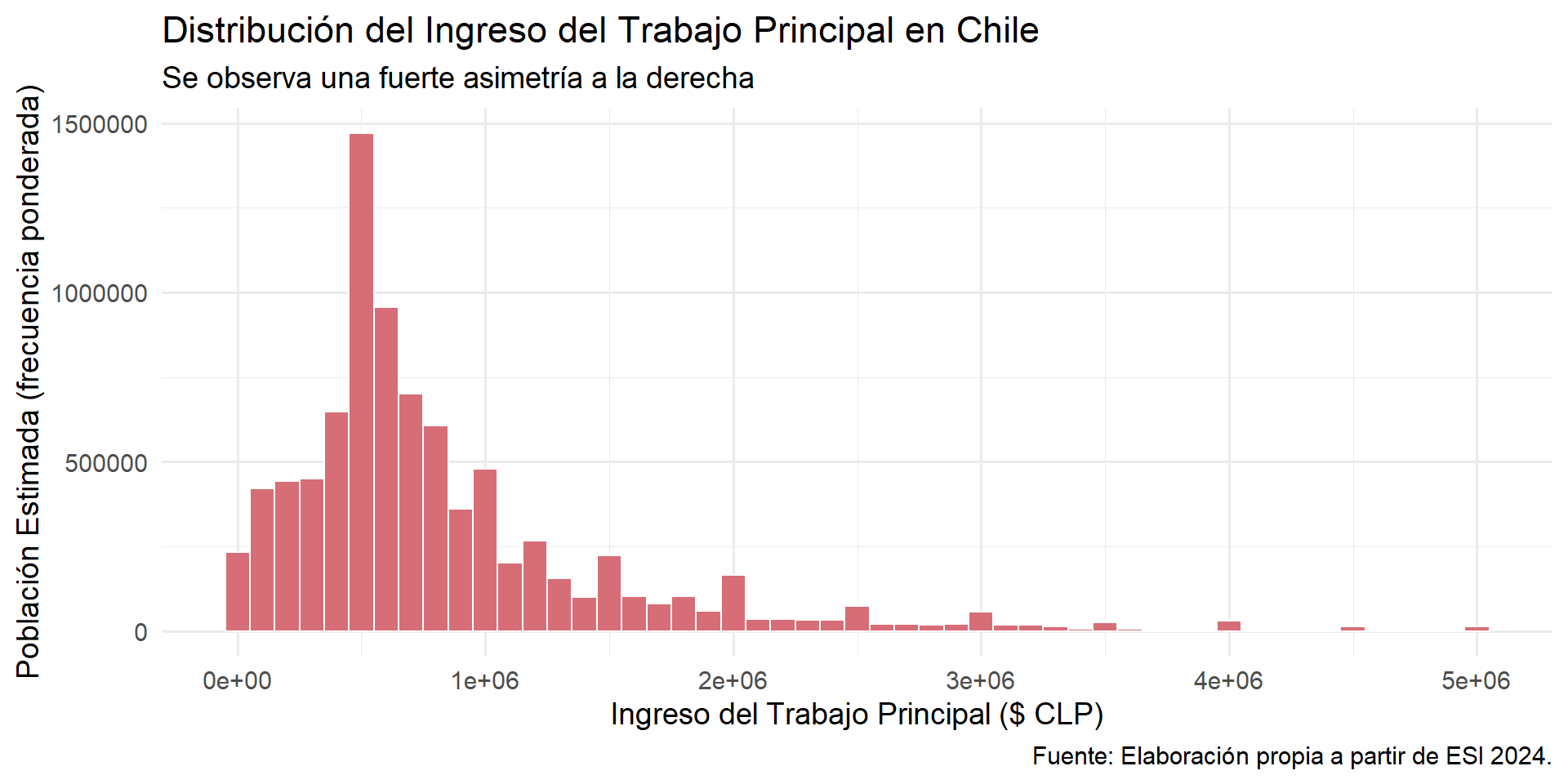
Ingreso del Trabajo Principal en Chile
Para ilustrar estos conceptos, usaremos la Encuesta Suplementaria de Ingresos (ESI) 2024 del INE. Nos centraremos en la variable ing_t_p (ingreso del trabajo principal) para los ocupados de referencia.
La Fuente de Datos: Encuesta Suplementaria de Ingresos (ESI)
¿Qué es? La ESI es un módulo que se aplica anualmente (en el trimestre octubre-diciembre) a una submuestra de los hogares que participan en la Encuesta Nacional de Empleo (ENE). Es la principal fuente de datos sobre ingresos en Chile.
Objetivo Principal: Caracterizar en detalle los ingresos de las personas y los hogares, yendo mucho más allá de lo que la ENE puede capturar por sí sola. Mide:
- Ingresos del trabajo principal y secundario.
- Ingresos de fuentes no laborales (jubilaciones, arriendos, etc.).
- Ingresos por trabajador/a por cuenta propia.
Relevancia Sociológica: Los datos de la ESI son cruciales para analizar la desigualdad económica, la brecha salarial de género y la estructura del mercado laboral en Chile. Cuando leemos en las noticias sobre la “mediana del ingreso” en el país, esa cifra proviene de esta encuesta.
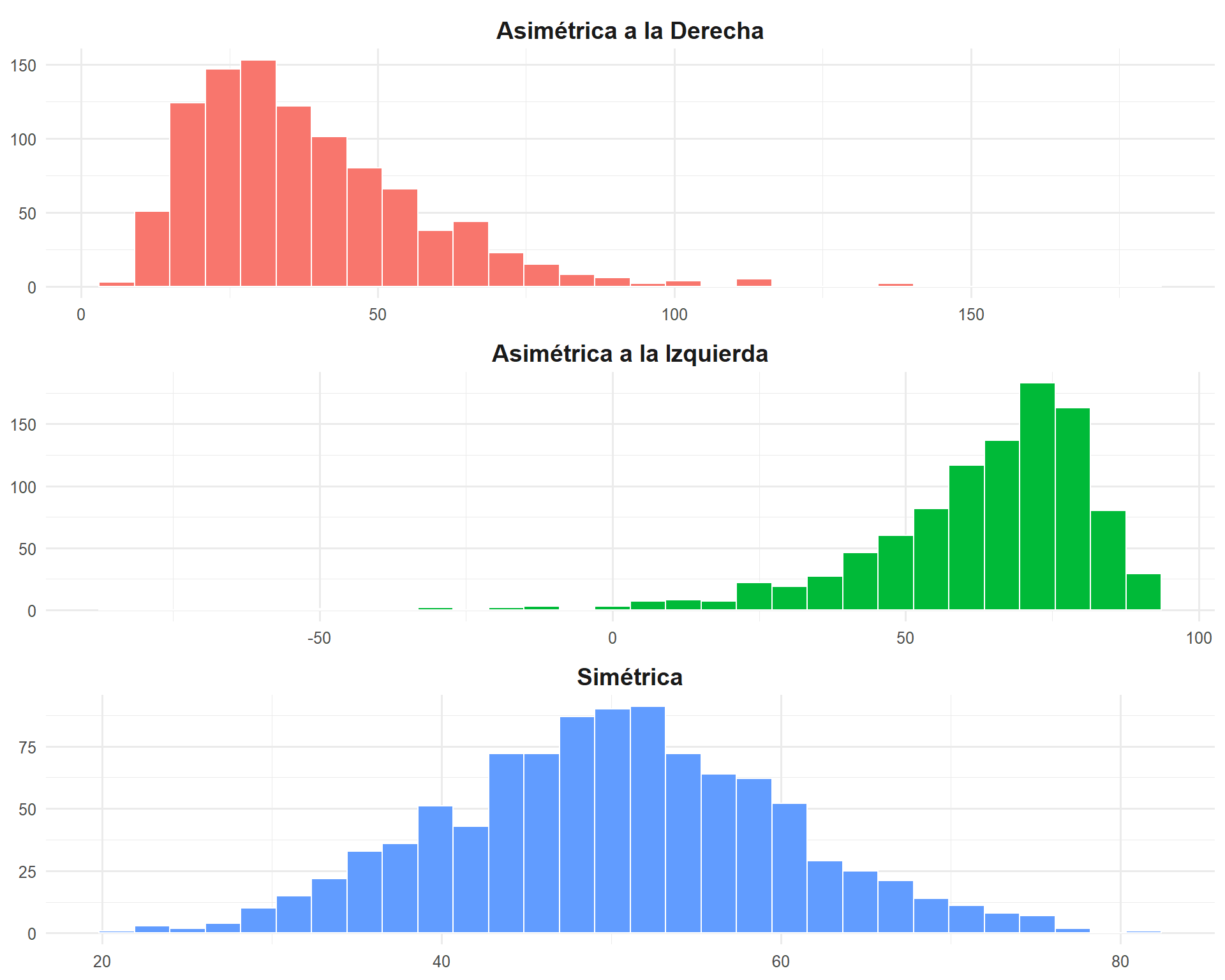
Interpretando la Forma: Asimetría (Sesgo)
La asimetría describe si la distribución está “cargada” o tiene una cola más larga hacia un lado.
Simétrica: Las colas izquierda y derecha son un espejo aproximado. La mayoría de los casos se agrupan simétricamente alrededor del centro.
Asimétrica a la derecha (sesgo positivo): La cola derecha es mucho más larga. Indica la presencia de muchos valores bajos/medios y unos pocos valores muy altos. Ejemplo sociológico clásico: el ingreso.
Asimétrica a la izquierda (sesgo negativo): La cola izquierda es mucho más larga. Indica muchos valores altos y pocos valores muy bajos. Ejemplo: notas en un examen que resultó ser muy fácil.
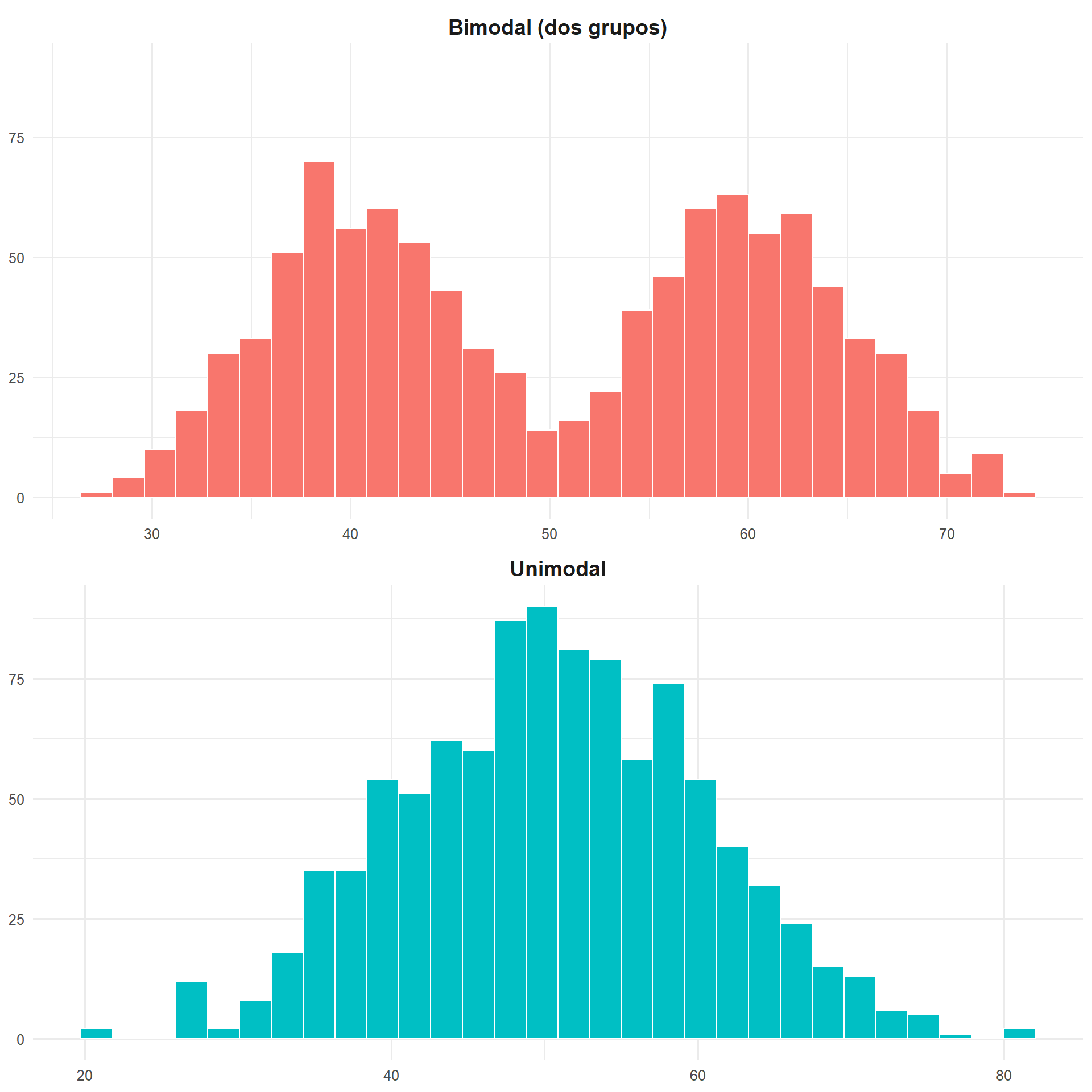
Interpretando la Forma: Modalidad
La modalidad se refiere al número de picos o modas que tiene una distribución.
Unimodal: La distribución tiene un solo pico principal. Es la forma más común, indicando que hay un valor o rango de valores claramente más frecuente que los demás.
Bimodal: La distribución tiene dos picos distintos. A menudo es una señal importante de que nuestros datos provienen de dos subgrupos diferentes que no hemos separado.
- Ejemplo: La distribución de estaturas en una muestra que mezcla hombres y mujeres probablemente será bimodal.
Multimodal: Tiene varios picos.
3. Medidas de Centro y Dispersión Robustas
¿Qué es una Medida Robusta?
Una medida estadística es robusta si no se ve afectada significativamente por la presencia de valores extremos (outliers) o por la asimetría de la distribución.
Ejemplo:
- Datos:
1, 2, 3, 4, 100 - La presencia del
100es un outlier. - Una medida robusta del centro debería estar cerca de
3, ignorando la influencia desproporcionada del100.
Hoy nos centraremos en las medidas robustas, que son ideales para describir distribuciones como la del ingreso.
La Mediana (M o Q2): El Centro Geométrico
La mediana es el valor que se encuentra en el punto medio exacto de los datos, una vez que han sido ordenados de menor a mayor.
- Definición: Es el percentil 50. Deja al 50% de las observaciones por debajo y al 50% por encima.
- Propiedad Clave: Es una medida de centro robusta. Su valor depende de la posición de los datos, no de su magnitud.
Ejemplo:
- Datos ordenados:
1, 2, **3**, 4, 100-> La mediana es 3. - Datos ordenados:
1, 2, **3**, 4, 10000-> La mediana sigue siendo 3.
El outlier no afecta a la mediana. Por eso es la medida preferida para describir el “ingreso típico” en una población.
Cuartiles y Rango Intercuartil (IQR)
Así como la mediana divide los datos en dos mitades, los cuartiles los dividen en cuatro partes iguales.
- Primer Cuartil (Q1): Es el percentil 25. Deja al 25% de los datos por debajo.
- Tercer Cuartil (Q3): Es el percentil 75. Deja al 75% de los datos por debajo.
A partir de los cuartiles, construimos la principal medida de dispersión robusta:
- Rango Intercuartil (IQR): Es la distancia entre el tercer y el primer cuartil (
IQR = Q3 - Q1). - Interpretación: El IQR representa el rango en el que se encuentra el 50% central de los datos. Al igual que la mediana, es una medida de dispersión robusta porque ignora los valores en las colas de la distribución.
Percentiles: Más Allá de los Cuartiles
Los cuartiles son solo un tipo de percentil (o cuantil), un concepto más general y flexible para describir la posición de un valor dentro de una distribución ordenada.
- Definición General: El percentil p es el valor por debajo del cual se encuentra el p% de las observaciones.
- La mediana es el percentil 50.
- El primer cuartil (Q1) es el percentil 25.
- El tercer cuartil (Q3) es el percentil 75.
Ejemplo: Los Quintiles de Ingreso
En sociología y políticas públicas, es muy común dividir a la población en cinco grupos de igual tamaño (20% cada uno). A estos grupos se les llama quintiles. Para definirlos, calculamos los percentiles 20, 40, 60 y 80.
Ejemplo con la ESI 2024:
| Percentil | Ingreso Límite |
|---|---|
| P20 | $400.000 |
| P40 | $548.629 |
| P60 | $750.000 |
| P80 | $1.200.000 |
- Una persona en el primer quintil gana hasta $400.000.
- Una persona en el quinto quintil (el 20% más rico) gana más de $1.200.000.
Podemos usar cualquier percentil para analizar la desigualdad. Por ejemplo, el percentil 99 nos diría cuál es el ingreso del 1% más rico de la población.
El Resumen de Cinco Números y el Boxplot
El resumen de cinco números es el conjunto estándar de estadísticas robustas para describir una variable cuantitativa.
Componentes:
- Mínimo
- Primer Cuartil (Q1)
- Mediana (M o Q2)
- Tercer Cuartil (Q3)
- Máximo
Este resumen se visualiza directamente a través de un diagrama de caja y bigotes o boxplot.
El Resumen de Cinco Números en la Práctica
Apliquemos estos conceptos a nuestra variable ing_t_p (ingreso del trabajo principal) de la ESI 2024. Este es el resumen numérico estándar para describir una distribución, especialmente si es asimétrica como la del ingreso.
Componentes: Mínimo, Primer Cuartil (Q1), Mediana, Tercer Cuartil (Q3) y Máximo.
| Medida | Ingreso Mensual |
|---|---|
| Mínimo | 2.993 |
| Q1 (Percentil 25) | 461.456 |
| Mediana (Percentil 50) | 626.045 |
| Q3 (Percentil 75) | 1.009.749 |
| Máximo | 60.756.649 |
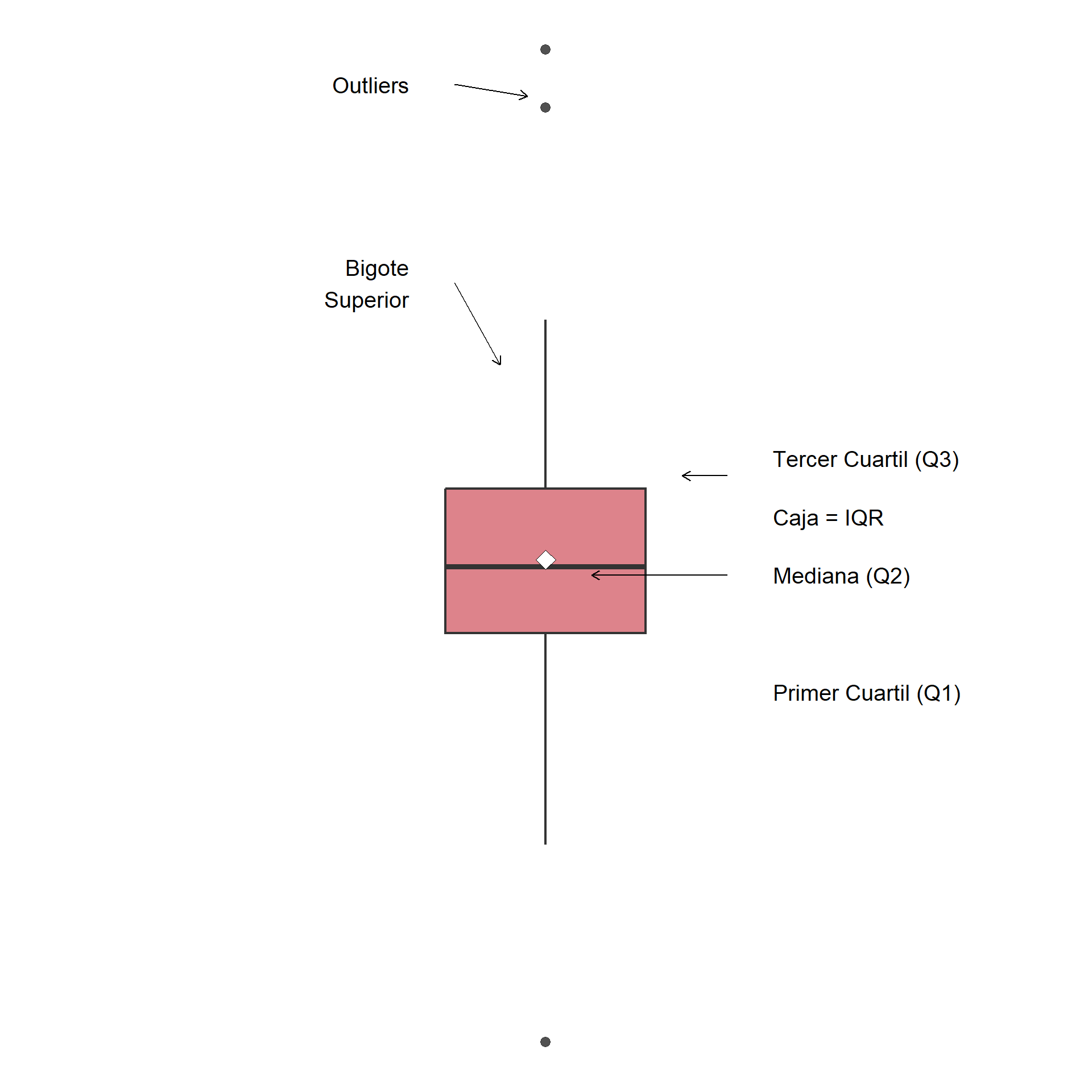
La Anatomía de un Boxplot
Un diagrama de caja y bigotes o boxplot es la visualización directa del resumen de cinco números y una de las herramientas más informativas de la estadística descriptiva.
- La Caja: Representa el Rango Intercuartil (IQR). Su longitud es una medida visual de la dispersión del 50% central de los datos.
- La Línea Central: Marca la mediana (Q2 o percentil 50).
- Los Bigotes: Se extienden hasta los valores mínimo y máximo “típicos” (generalmente 1.5 veces el IQR desde la caja).
- Los Puntos: Representan valores atípicos (outliers), que son observaciones que caen más allá de los bigotes, permitiendo identificarlos fácilmente.
El Boxplot de Ingreso del Trabajo Principal
Apliquemos el boxplot a la variable de ingreso de la ESI 2024. Este gráfico nos permite ver de un solo vistazo la forma, el centro, la dispersión y la enorme cantidad de outliers.
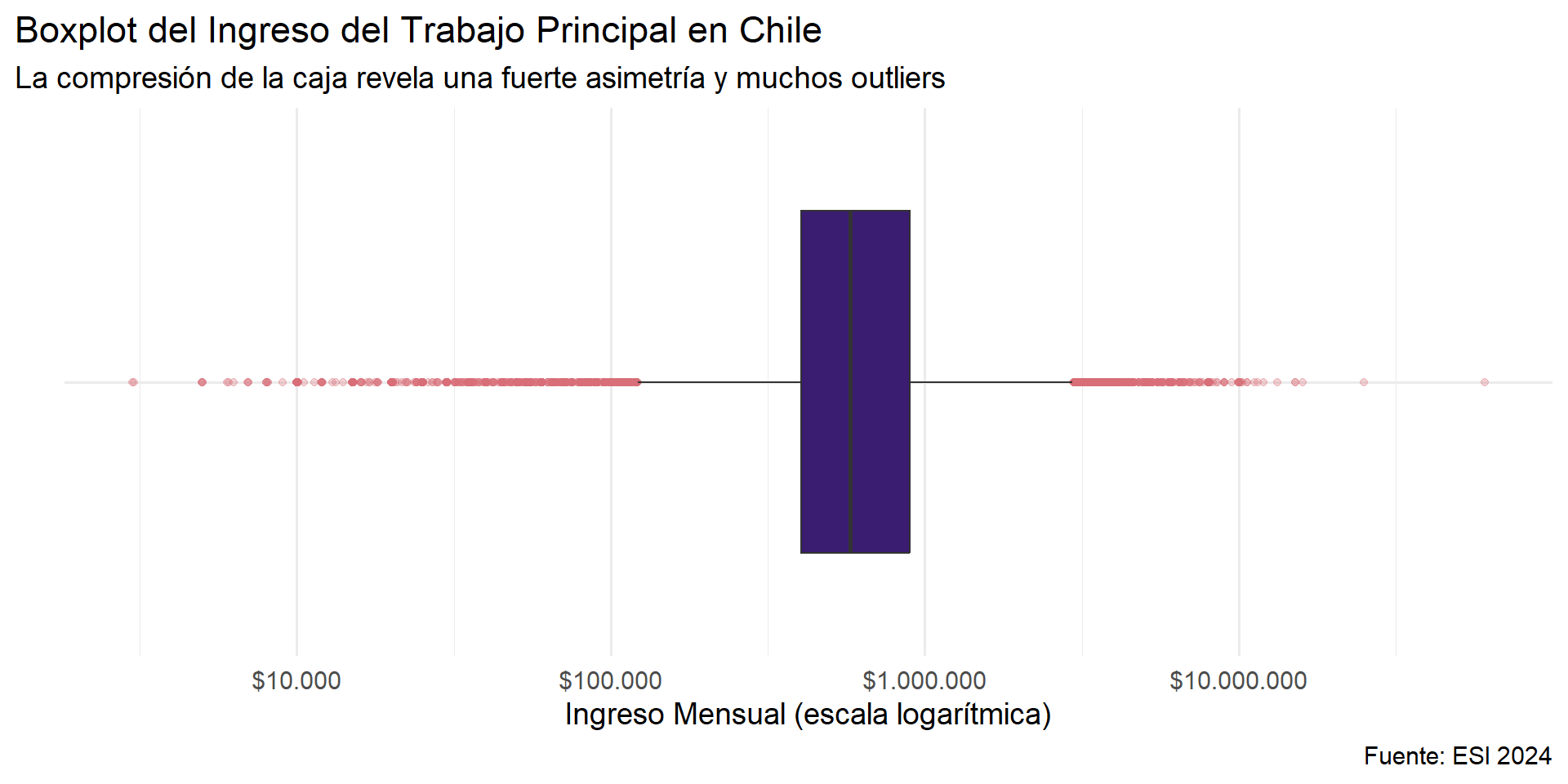
La Escala Logarítmica
En el gráfico anterior, para poder visualizar la distribución del ingreso, aplicamos una transformación al eje: una escala logarítmica. Esta es una herramienta fundamental cuando trabajamos con variables que, como el ingreso, tienen una fuerte asimetría positiva.
- El Problema de la Asimetría: Cuando unos pocos valores muy altos (como los ingresos de las personas más ricas) son miles de veces más grandes que la mayoría, “aplastan” el resto del gráfico. La caja y los bigotes del boxplot, o un histograma, se comprimen tanto en la parte inferior que se vuelven casi invisibles, y perdemos toda la información sobre el 50% o 75% inferior de la población.
La Escala Logarítmica
¿Qué hace una Escala Logarítmica?
Una escala estándar (lineal) muestra los valores en sus unidades absolutas. La distancia entre 100.000 y 200.000 es la misma que entre 2.000.000 y 2.100.000.
Una escala logarítmica, en cambio, representa órdenes de magnitud. La distancia en el eje es la misma para cada multiplicación (usualmente x10). La distancia entre $100.000 y $1.000.000 (x10) es la misma que entre $1.000.000 y $10.000.000 (x10).
El Efecto Práctico:
- Comprime la cola derecha: Reduce visualmente la distancia entre los valores altos y extremos.
- Expande la base: Estira la parte inferior de la distribución, permitiéndonos ver con claridad la posición de la mediana, la forma de la caja (el IQR) y la distribución de la mayoría de los casos.
- Facilita la interpretación: Nos ayuda a pensar en términos de cambios relativos (ej. “duplicar el ingreso”) en lugar de cambios absolutos, lo cual puede ser más relevante sociológicamente.
Cierre y Próximos Pasos
Resumen de la sesión de hoy:
- Introdujimos el marco Forma-Centro-Dispersión para describir variables cuantitativas.
- Aprendimos a usar histogramas para visualizar la forma (asimetría, modalidad).
- Definimos y calculamos las medidas robustas de centro (mediana) y dispersión (IQR).
- Vimos cómo el resumen de cinco números se traduce en un boxplot, una poderosa herramienta visual.
En el práctico de hoy:
- Aplicarán estas técnicas en R para describir variables de la Encuesta CASEN, usando
geom_histogram,geom_boxplot,summary()yquantile().
Adelanto de la próxima clase:
- Exploraremos el otro par de medidas descriptivas: la media y la desviación estándar. Veremos por qué no son robustas y cuándo es apropiado usarlas.
