Análisis Cuantitativo Bivariado: Dispersión y Correlación

0. Objetivos del Práctico

En este práctico cerraremos el ciclo de análisis bivariado explorando la relación entre dos variables numéricas (cuantitativas). Al finalizar, serás capaz de:

Diagnosticar visualmente la relación entre variables usando gráficos de dispersión (scatterplots), identificando patrones lineales, curvos y problemas de densidad de datos.
Interpretar líneas de tendencia (lm para relaciones lineales vs loess para relaciones locales) para detectar comportamientos complejos.
Cuantificar la fuerza de una asociación lineal utilizando el Coeficiente de Correlación de Pearson (\(r\)).
Gestionar matrices de correlación de manera eficiente y ordenada utilizando el paquete corrr.
Integrar estas herramientas para poner a prueba hipótesis sobre la distribución del tiempo y la carga laboral.

1. Contexto y Preparación de Datos

1.1 Preparación del Entorno y Datos

Paso 1: Organiza tu entorno Como siempre, asegúrate de estar trabajando dentro de tu Proyecto de RStudio y de tener una carpeta datos.

Paso 2: Descarga la Base de Datos Descarga la base de datos de la ENUT 2023 desde el siguiente enlace y guarda el archivo .zip en tu carpeta datos:

Enlace de descarga: Base de datos ENUT 2023 (formato R)

Paso 3: Carga de Paquetes y Datos

Como es habitual, cargamos nuestros paquetes. Hoy incorporamos corrr, una herramienta moderna del ecosistema tidyverse diseñada específicamente para trabajar con correlaciones de forma ordenada y compatible con el flujo de datos que ya conoces.

# Cargar paquetes esenciales
library(tidyverse)  # Manipulación y gráficos
library(haven)      # Manejo de etiquetas
library(rio)        # Importación de datos
library(knitr)      # Tablas estáticas
library(kableExtra) # Estilo de tablas

# Paquete nuevo para este práctico
library(corrr)      # Análisis de correlaciones estilo 'tidy'

Cargamos la base de datos:

# Carga Manual (Método recomendado desde tu carpeta de proyecto)
enut <- rio::import("datos/250403-ii-enut-bdd-r-v2.zip", which = "250403-ii-enut-bdd-r-v2.RDS")

# Carga automática (Solo para reproducción del documento)
enut <- rio::import("https://www.ine.gob.cl/docs/default-source/uso-del-tiempo-tiempo-libre/bbdd/ii-enut/250403-ii-enut-bdd-r-v2.zip?sfvrsn=87682f16_7", which = "250403-ii-enut-bdd-r-v2.RDS")

1.2 Limpieza y Selección de Variables

Para analizar correlaciones, necesitamos variables puramente numéricas. Los códigos de “No aplica” (como 96, 99, etc.) actúan como ruido estadístico si no los tratamos, ya que R los interpretará como una cantidad de horas muy alta (96 horas) en lugar de una categoría administrativa.

Seleccionaremos variables clave sobre ciclo de vida (edad) y cargas de trabajo (remunerado, doméstico y de cuidados).

enut_cuant <- enut %>%
  filter(tiempo == 1) %>% # Solo quienes respondieron el diario de actividades
  mutate(
    # 1. Limpieza: Convertir códigos administrativos a NA (Valores Perdidos)
    t_to_dt   = na_if(t_to_dt, 96),     # Trabajo en la ocupación
    t_tdnr_dt = na_if(t_tdnr_dt, 96),   # Trabajo doméstico no remunerado
    t_tcnr_dt = na_if(t_tcnr_dt, 96),   # Trabajo de cuidados no remunerado
    
    # 2. Creación: Variable sintética de Carga Global de Trabajo No Remunerado
    t_nr_total = t_tdnr_dt + t_tcnr_dt,
    
    # 3. Factores: Para comparaciones grupales posteriores
    sexo_factor = as_factor(sexo),
    grupo_edad  = case_when(
      edad <= 29 ~ "Joven",
      edad <= 59 ~ "Adulto",
      edad >= 60 ~ "Adulto Mayor"
    )
  ) %>%
  # 4. Selección: Nos quedamos con un dataset manejable
  select(id_persona, fe_cut, edad, sexo_factor, grupo_edad, 
         t_to_dt, t_tdnr_dt, t_tcnr_dt, t_nr_total)

2. El Análisis Visual: El Gráfico de Dispersión

Antes de calcular cualquier número, siempre debemos visualizar. El coeficiente de correlación asume una línea recta, por lo que puede ser engañoso si la relación es curva o si hay valores atípicos (outliers).

Pregunta Sociológica: ¿Cómo cambia la carga de trabajo doméstico a medida que las personas envejecen? ¿Es una acumulación lineal constante o varía por etapas de vida?

Utilizaremos geom_point() para los datos y geom_smooth() para comparar tendencias.

# Construcción del gráfico capa por capa
ggplot(enut_cuant, aes(x = edad, y = t_tdnr_dt)) +
  
  # Capa 1: Los Puntos 
  # Usamos alpha = 0.1 para manejar el 'overplotting' (muchos puntos encimados).
  # Esto hace que los puntos sean semitransparentes: zonas más oscuras indican mayor densidad de datos.
  geom_point(alpha = 0.1, color = "#2c3e50") +
  
  # Capa 2: Tendencia Lineal 
  # method = "lm" fuerza una línea recta (Linear Model)
  geom_smooth(method = "lm", color = "#e74c3c", se = FALSE, linewidth = 1) +
  
  # Capa 3: Tendencia Local
  # method = "loess" se adapta a las curvas de los datos
  geom_smooth(method = "loess", color = "#3498db", se = FALSE, linetype = "dashed", linewidth = 1) +
  
  # Etiquetas y Estética
  labs(
    title = "Ciclo de Vida y Trabajo Doméstico",
    subtitle = "Comparación entre ajuste lineal (rojo) y ajuste no-lineal (azul)",
    x = "Edad (años)",
    y = "Horas diarias dedicadas al trabajo doméstico (TDNR)"
  ) +
  theme_minimal()

## `geom_smooth()` using formula = 'y ~ x'
## `geom_smooth()` using formula = 'y ~ x'

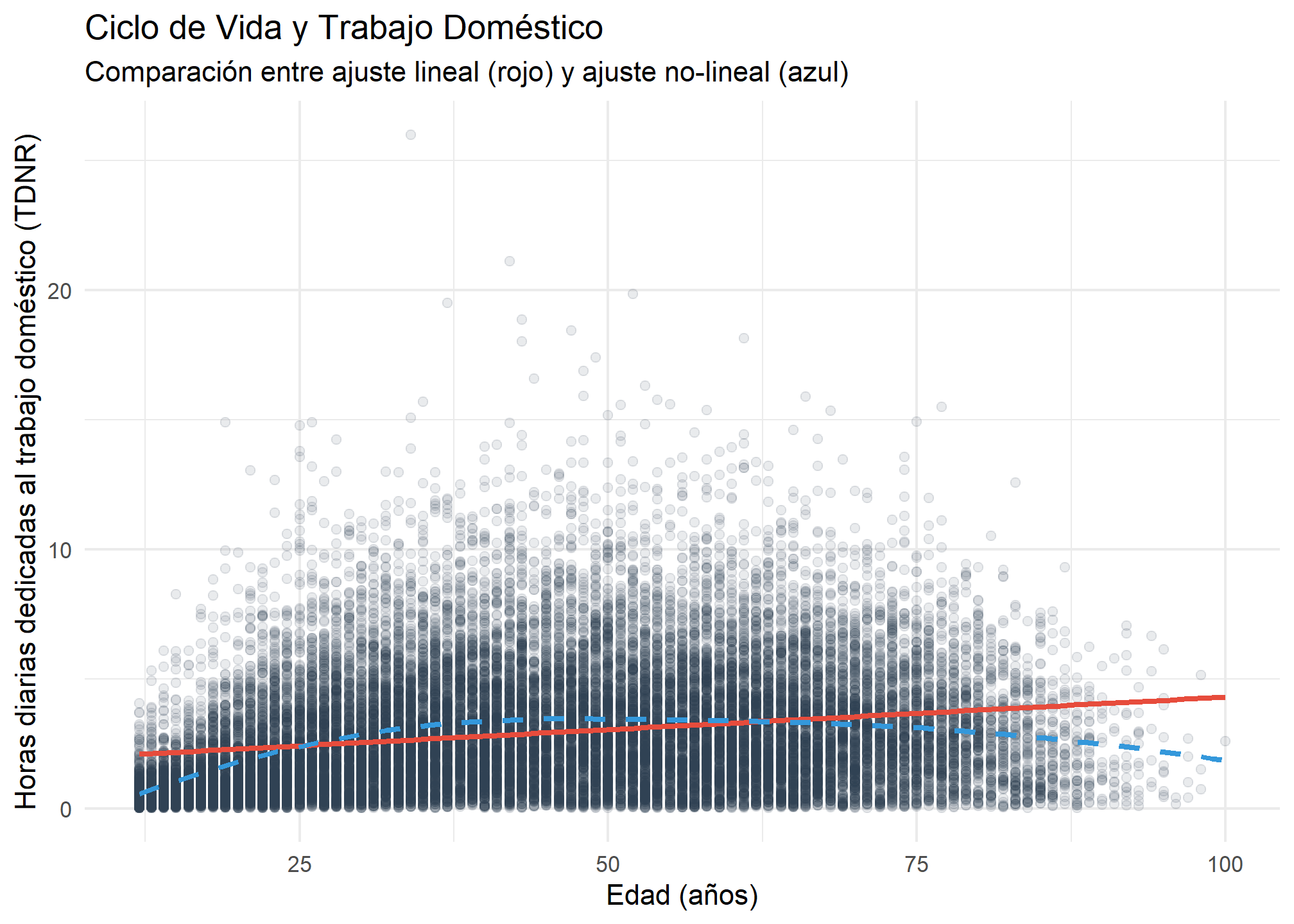
Interpretación

Observa las diferencias entre las líneas de tendencia:

Línea Roja (Lineal): Muestra una pendiente positiva suave. Nos dice que, en general, a mayor edad, mayor trabajo doméstico.
Línea Azul (Loess): Nos cuenta una historia más rica. El trabajo doméstico aumenta rápidamente entre los 15 y los 30 años (independencia, formación de hogares), se mantiene alto y estable durante la adultez, y comienza a decaer levemente en la vejez avanzada.

En este caso la línea roja (correlación lineal) “aplana” la realidad. Si solo calculamos el número, perdemos de vista la aceleración inicial y la caída final que nos muestra la línea azul.

Tip: Los valores atípicos (outliers) pueden distorsionar fuertemente la línea recta. Siempre mira el gráfico para ver si unos pocos puntos extremos están “tirando” de la línea.

3. Cuantificando la Relación: Correlación de Pearson

El coeficiente \(r\) de Pearson mide la fuerza y dirección de una relación lineal. Varía entre -1 (negativa perfecta) y +1 (positiva perfecta).

3.1 Cálculo Simple con R Base

Calcularemos el coeficiente para las variables graficadas arriba. Es crucial usar el argumento use = "pairwise.complete.obs", que le indica a R que ignore los valores NA (perdidos) solo para el par de variables que está calculando en ese momento.

# Calculamos la correlación ignorando los NA
correlacion_edad_tdnr <- cor(enut_cuant$edad, enut_cuant$t_tdnr_dt, use = "pairwise.complete.obs")

# Imprimimos el resultado redondeado
round(correlacion_edad_tdnr, 3)

## [1] 0.204

Interpretación del Resultado: El resultado es 0.204. ¿Cómo leemos esto?

Signo (+): Es positivo. Confirma que existe una tendencia al aumento del trabajo doméstico con la edad.
Magnitud (0.2): Es una correlación baja a moderada.
Sociológicamente: Esto indica que, aunque la edad influye, no determina por sí sola cuánto lavas o cocinas. Hay mucha variabilidad (dispersión) en los datos que la edad no explica (como el género, el tamaño del hogar, o la clase social).

Recuerda: Correlación no implica causalidad. Que dos cosas se muevan juntas no significa que una cause la otra.

3.2 Actividad 1: Relaciones entre Tipos de Trabajo

Instrucción: Ahora analiza dos variables de carga de trabajo. Calcula e interpreta la correlación entre las horas de trabajo doméstico (t_tdnr_dt) y las horas de trabajo de cuidados (t_tcnr_dt).

¿Es positiva o negativa?
¿Es más fuerte o más débil que la relación con la edad?
Reflexión: ¿Significa esto que las tareas se acumulan (quien cocina también cuida) o se sustituyen?

# Escribe tu código aquí usando cor(..., use = "pairwise.complete.obs")

4. Matrices de Correlación con `corrr`

En las ciencias sociales rara vez analizamos solo dos variables aisladas. Necesitamos ver el sistema completo. La función base cor() devuelve una matriz difícil de leer y poco amigable. El paquete corrr soluciona esto devolviendo un tibble (dataframe) fácil de manipular, filtrar y visualizar con ggplot2.

4.1 Creación de la Matriz Tidy

# 1. Selección de variables y cálculo
matriz_tidy <- enut_cuant %>%
  select(edad, t_to_dt, t_tdnr_dt, t_tcnr_dt) %>%
  correlate() # Función clave de corrr para calcular la matriz

## Correlation computed with
## • Method: 'pearson'
## • Missing treated using: 'pairwise.complete.obs'

# 2. Visualización elegante de la tabla
matriz_tidy %>%
  shave() %>% # Elimina la mitad superior duplicada (espejo) para limpiar la vista
  fashion()   # Formatea decimales para lectura humana y redondea inteligentemente

##        term edad t_to_dt t_tdnr_dt t_tcnr_dt
## 1      edad                                 
## 2   t_to_dt  .02                            
## 3 t_tdnr_dt  .20    -.20                    
## 4 t_tcnr_dt -.15    -.15       .20

4.2 Visualización de la Matriz (`rplot`)

Podemos visualizar la intensidad y dirección de todas las correlaciones simultáneamente.

matriz_tidy %>%
  rplot(colors = c("#e74c3c", "white", "#3498db")) + # Rojo (neg) - Blanco - Azul (pos)
  labs(title = "Mapa de Correlaciones: Uso del Tiempo")

## Warning: `aes_string()` was deprecated in ggplot2 3.0.0.
## ℹ Please use tidy evaluation idioms with `aes()`.
## ℹ See also `vignette("ggplot2-in-packages")` for more information.
## ℹ The deprecated feature was likely used in the corrr package.
##   Please report the issue at <https://github.com/tidymodels/corrr/issues>.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

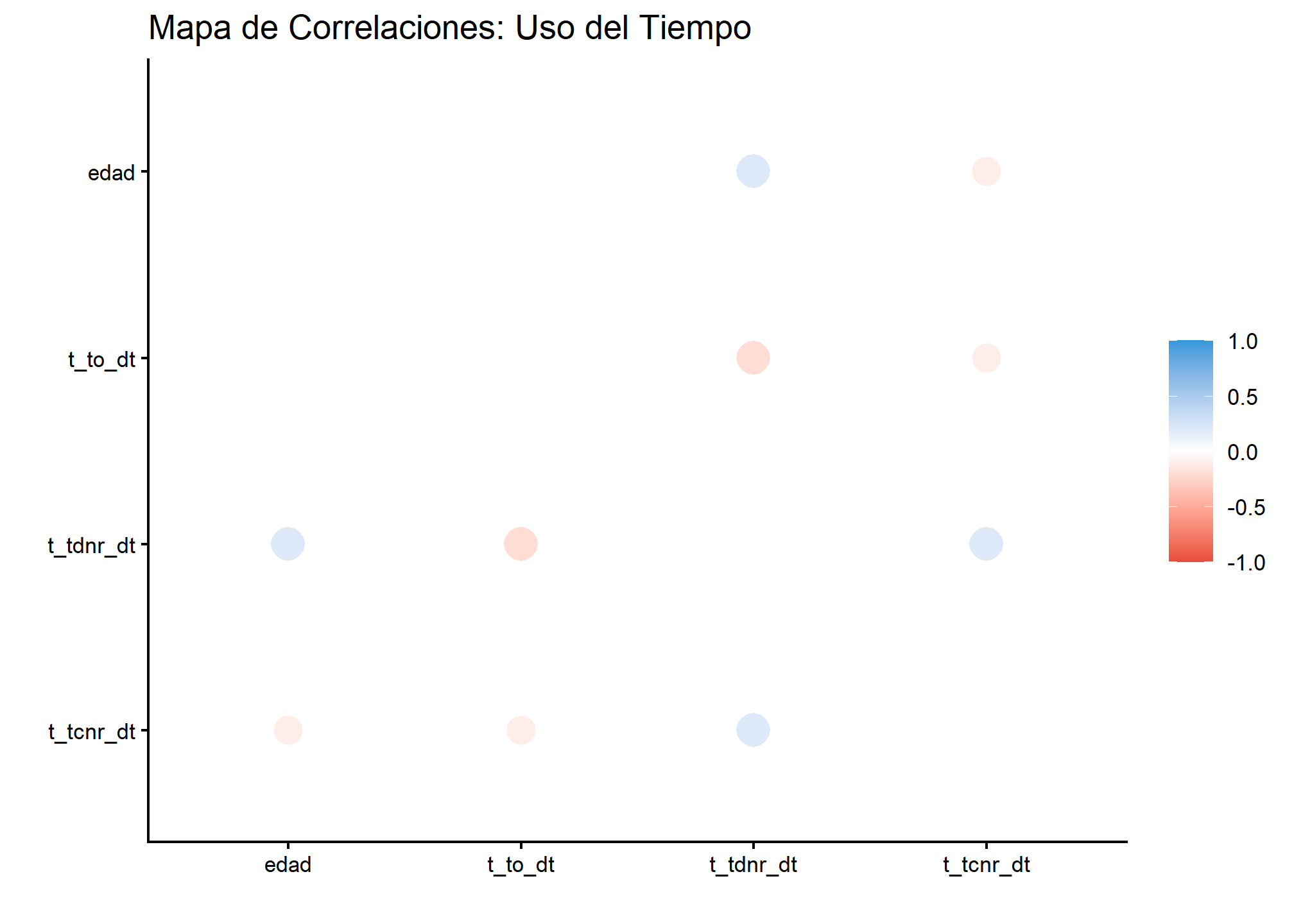
Interpretación Detallada del Mapa: Mirando la tabla y el gráfico, podemos extraer conclusiones sistémicas:

Trabajo Doméstico vs. Cuidados (\(r = 0.20\), Azul): Existe una correlación positiva. Esto sugiere una acumulación de roles: las personas que dedican tiempo a cuidar (niños/ancianos) también tienden a dedicar tiempo a las tareas domésticas. No son tareas excluyentes, sino superpuestas.
Trabajo Remunerado vs. No Remunerado (\(r = -0.20\), Rojo): Observa la fila de t_to_dt frente a t_tdnr_dt. La correlación es negativa (\(-0.20\)). Esto indica un conflicto de tiempo: quienes pasan más horas en el empleo tienden a hacer menos trabajo doméstico. Sin embargo, la magnitud no es muy alta (no es -0.8), lo que sugiere que la reducción del trabajo doméstico no es proporcional a las horas trabajadas fuera de casa (la famosa “doble jornada”).

5. Actividad de Desafío Final (Integradora)

Pregunta de Investigación: Vamos a poner a prueba estadísticamente la hipótesis de la “Doble Jornada” vs. la “Sustitución”.

Hipótesis de Sustitución Pura: Si trabajo más horas fuera de casa, debería reducir mis horas domésticas drásticamente (correlación negativa muy fuerte).
Hipótesis de Doble Jornada: Aunque trabaje fuera, sigo manteniendo una carga alta en casa (correlación débil o cercana a cero).

Instrucciones:

Crea una nueva variable trabajo_total_nr (ya disponible si ejecutaste el paso 1.2).
Filtra la base para analizar solo a personas ocupadas (t_to_dt > 0), ya que queremos ver el efecto del empleo.
Genera un gráfico de dispersión facetado por sexo:
- Eje X: t_to_dt (Horas remuneradas)
- Eje Y: trabajo_total_nr (Horas no remuneradas)
- Usa facet_wrap(~ sexo_factor)
- Añade geom_smooth(method = "lm").
Calcula la correlación (cor) agrupada por sexo_factor.

Interpretación Final: Compara los coeficientes de hombres y mujeres.

Si el coeficiente de los hombres es más negativo (ej. -0.4) que el de las mujeres (ej. -0.1), ¿qué significa? Significaría que los hombres logran “deshacerse” de las tareas domésticas cuando encuentran empleo, mientras que las mujeres las mantienen (doble jornada). ¿Qué dicen tus datos?

# 1. Preparación de datos (filtro)
# data_filtrada <- enut_cuant %>% filter(...)

# 2. Gráfico facetado por sexo (Visualización de la pendiente)
# ggplot(data_filtrada, aes(x = ..., y = ...)) +
#   geom_point(...) +
#   geom_smooth(...) +
#   facet_wrap(...)

# 3. Cálculo de correlaciones por grupo (Cuantificación de la pendiente)
# Pista: usa group_by() %>% summarise(r = cor(..., use = "pairwise.complete.obs"))
# data_filtrada %>%
#   group_by(...) %>%
#   summarise(...)

# 4. Comentario de interpretación sociológica
# (Escribe aquí tu interpretación comparando los coeficientes)

Last updated on November 23, 2025