La Visualización como Argumento Sociológico con ggplot2

0. Objetivos del Práctico

El objetivo de este práctico es dominar la “Gramática de Gráficos” para construir visualizaciones de datos informativas y de alta calidad en R. Al finalizar, serás capaz de:

  • Argumentar por qué la visualización de datos es un paso indispensable en el análisis.
  • Construir gráficos en ggplot2 capa por capa, entendiendo la función de data, aes() y geom.
  • Crear los principales gráficos univariados y bivariados (geom_histogram, geom_bar, geom_point, geom_boxplot).
  • Aplicar mejores prácticas para crear gráficos claros, honestos y estéticamente pulcros.
  • Utilizar faceting (facet_wrap) para comparar distribuciones a través de múltiples categorías.

1. Contexto y Preparación de Datos

1.1 El “Porqué” de la Visualización

Como vimos en la clase, la visualización de datos no es un simple adorno. Es una forma de argumento sociológico y una herramienta de diagnóstico fundamental. AVimosen la clase como autores como Piketty y Bourdieu usan gráficos como el núcleo de sus teorías. Estadísticamente, graficar nuestros datos es la mejor forma de descubrir la verdadera forma de una distribución, que puede ocultarse detrás de estadísticos descriptivos similares.

1.2 Preparación del Entorno y Datos (CASEN 2022)

Como en prácticos anteriores, nuestro primer paso es asegurar un entorno de trabajo reproducible.

  1. Asegúrate de estar en tu Proyecto de RStudio y de tener una carpeta datos.
  2. Descarga la Base de Datos CASEN 2022 (formato SPSS) desde este enlace y guarda el archivo .sav en tu carpeta datos.

Carga de Paquetes

Cargamos los paquetes que necesitaremos para la sesión de hoy.

# Cargar los paquetes que usaremos hoy
library(tidyverse)
library(haven)

Carga de Datos

A continuación, hay dos formas de cargar los datos. Debes usar el Método 1 (Carga Manual).

Método 1: Carga Manual (Para tu trabajo) Este bloque de código carga la base de datos que guardaste en tu carpeta datos.

# Usamos read_sav() con la ruta relativa a nuestro proyecto
casen <- read_sav("datos/Base de datos Casen 2022 SPSS.sav")

Método 2: Carga Automática (Para reproducibilidad del documento) El siguiente bloque es para que este práctico se pueda generar automáticamente. No necesitas ejecutarlo si ya cargaste los datos con el método anterior.

# Código automático para cargar los datos desde la web
temp <- tempfile() 
download.file("https://observatorio.ministeriodesarrollosocial.gob.cl/storage/docs/casen/2022/Base%20de%20datos%20Casen%202022%20SPSS.sav.zip", temp)
casen <- haven::read_sav(unz(temp, "Base de datos Casen 2022 SPSS.sav"))
unlink(temp); remove(temp)

2. Diagnóstico Visual: ¡Grafica Siempre tus Datos!

Vamos a demostrar con un ejemplo por qué los estadísticos resumen no son suficientes. Crearemos tres conjuntos de datos simulados que tienen la misma media y desviación estándar, pero formas muy diferentes.

# 1. Creamos los datos simulados
set.seed(123)
grupo_a <- tibble(valor = rnorm(500, 75, 10), grupo = "A: Simétrico (Unimodal)")
grupo_b <- tibble(valor = c(rnorm(250, 65, 5), rnorm(250, 85, 5)), grupo = "B: Bimodal (Dos grupos)")
grupo_c <- tibble(valor = rexp(500, 1/10) * 5 + 25, grupo = "C: Asimétrico (con Outliers)")

# Forzamos que los estadísticos sean casi idénticos por motivos pedagógicos
trio_enganoso <- bind_rows(grupo_a, grupo_b, grupo_c) %>%
  group_by(grupo) %>%
  mutate(valor = as.numeric(scale(valor)) * 10 + 75)

# 2. Calculamos los estadísticos descriptivos
trio_enganoso %>%
  summarise(
    Media = mean(valor),
    `Desv. Estándar` = sd(valor)
  )

## # A tibble: 3 × 3
##   grupo                        Media `Desv. Estándar`
##   <chr>                        <dbl>            <dbl>
## 1 A: Simétrico (Unimodal)         75             10.0
## 2 B: Bimodal (Dos grupos)         75             10  
## 3 C: Asimétrico (con Outliers)    75             10

# 3. Visualizamos los datos
ggplot(trio_enganoso, aes(x = valor)) +
  geom_histogram(fill = "#008080", color = "white", bins = 20) +
  facet_wrap(~grupo) +
  labs(title = "El Trío Engañoso: Mismos Estadísticos, Diferentes Distribuciones") +
  theme_minimal()

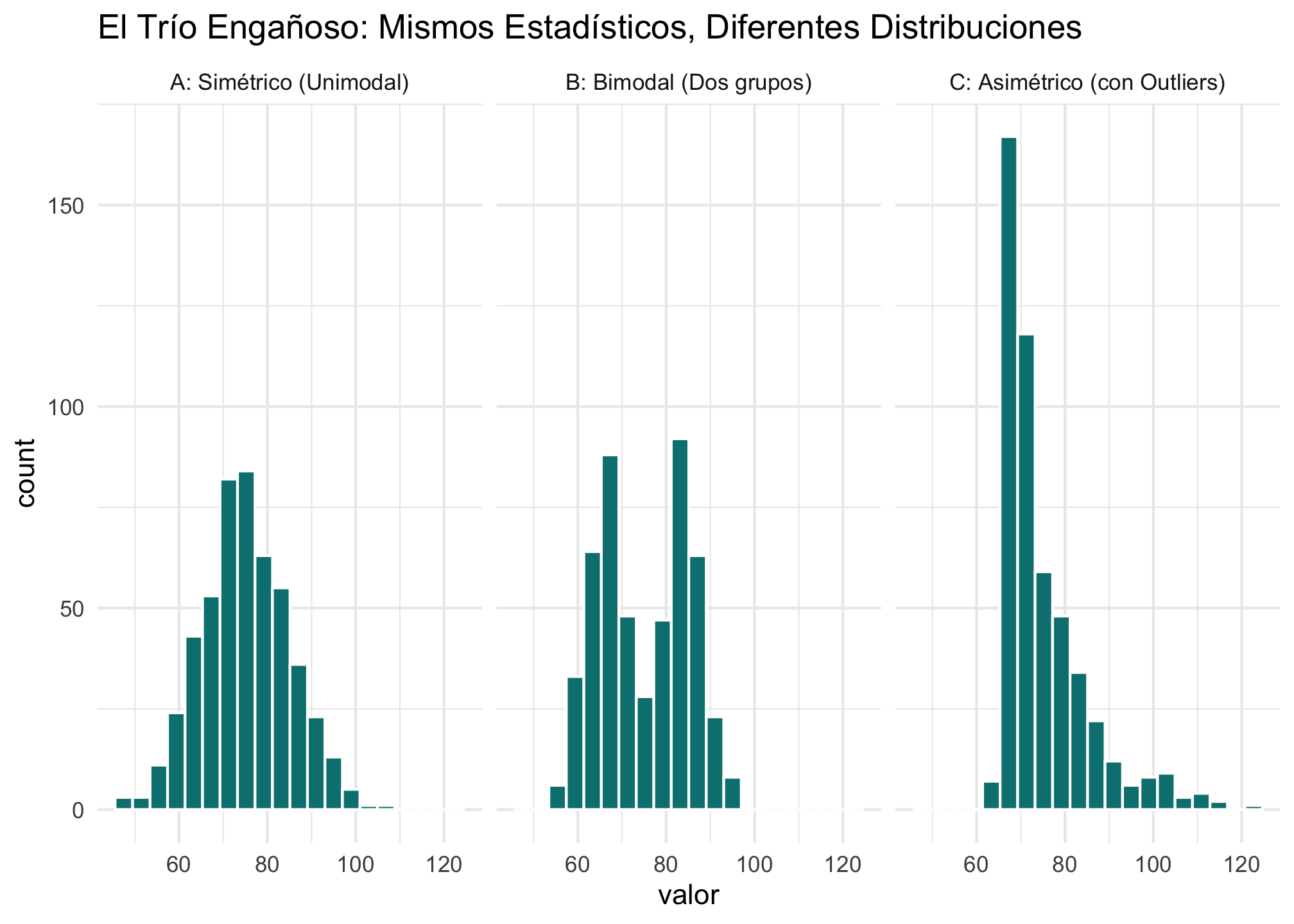Interpretación: La tabla muestra que los tres grupos son numéricamente casi idénticos. Sin embargo, los histogramas revelan realidades completamente distintas. El Grupo A es simétrico, el Grupo B claramente contiene dos subpoblaciones, y el Grupo C está fuertemente sesgado a la derecha. Esta es la razón por la que siempre debemos empezar visualizando nuestros datos.

3. La Gramática de Gráficos en la Práctica

Construiremos un histograma de edad capa por capa para entender la lógica de ggplot2.

# Capa 1: Los Datos y las Estéticas (aes). Crea un lienzo en blanco con el eje X definido.
p <- ggplot(data = casen, mapping = aes(x = edad))
p


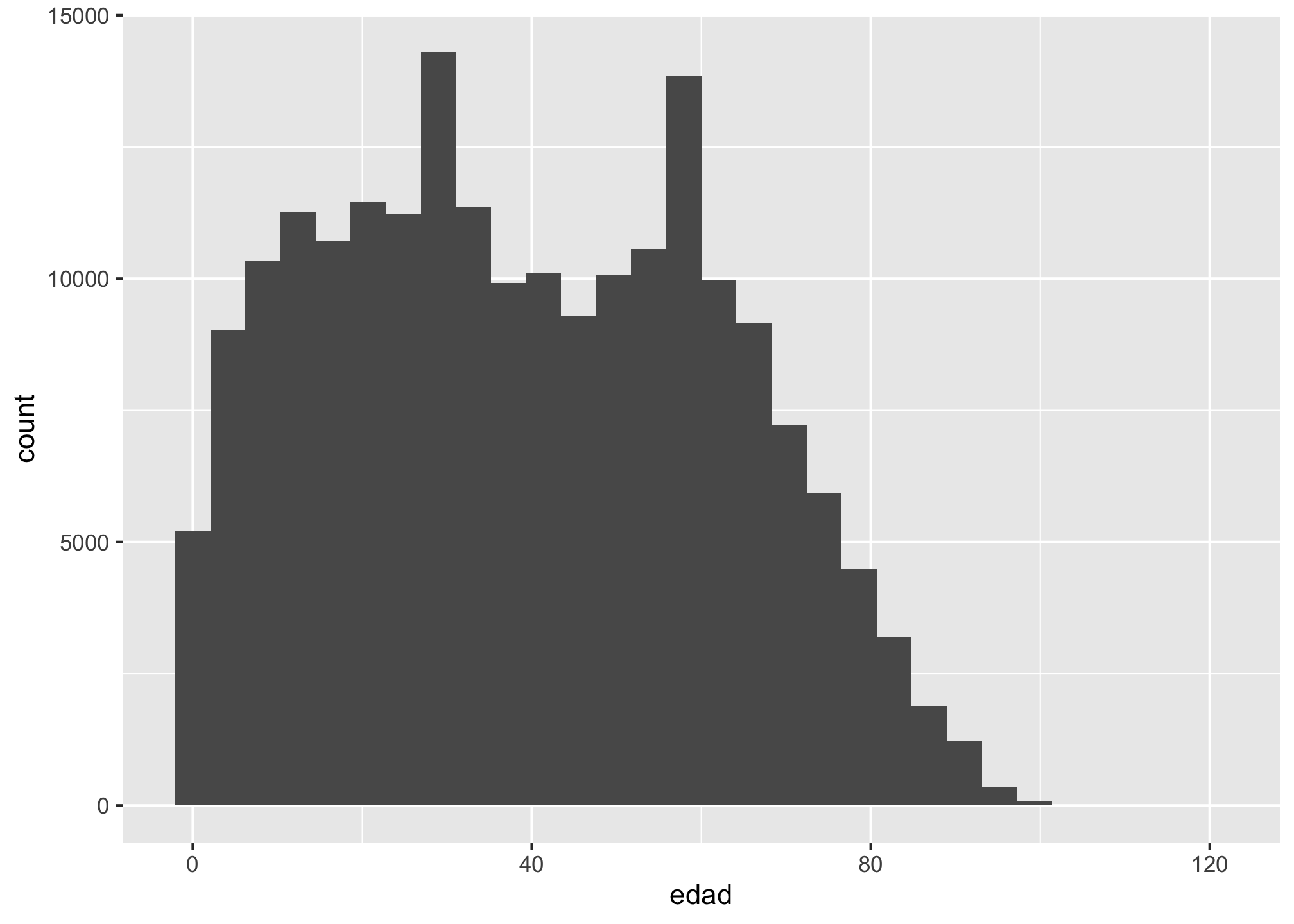
# Capa 2: La Geometría. Añadimos la capa que dibuja el histograma.
p <- p + geom_histogram() 
p

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.


# Capa 3: Personalización estética. Ajustamos colores y número de bins.
# p <- p + geom_histogram(fill = "#40E0D0", color = "white", bins = 30)
# (Para ver el cambio, tendríamos que volver a dibujar p. Lo haremos todo junto)

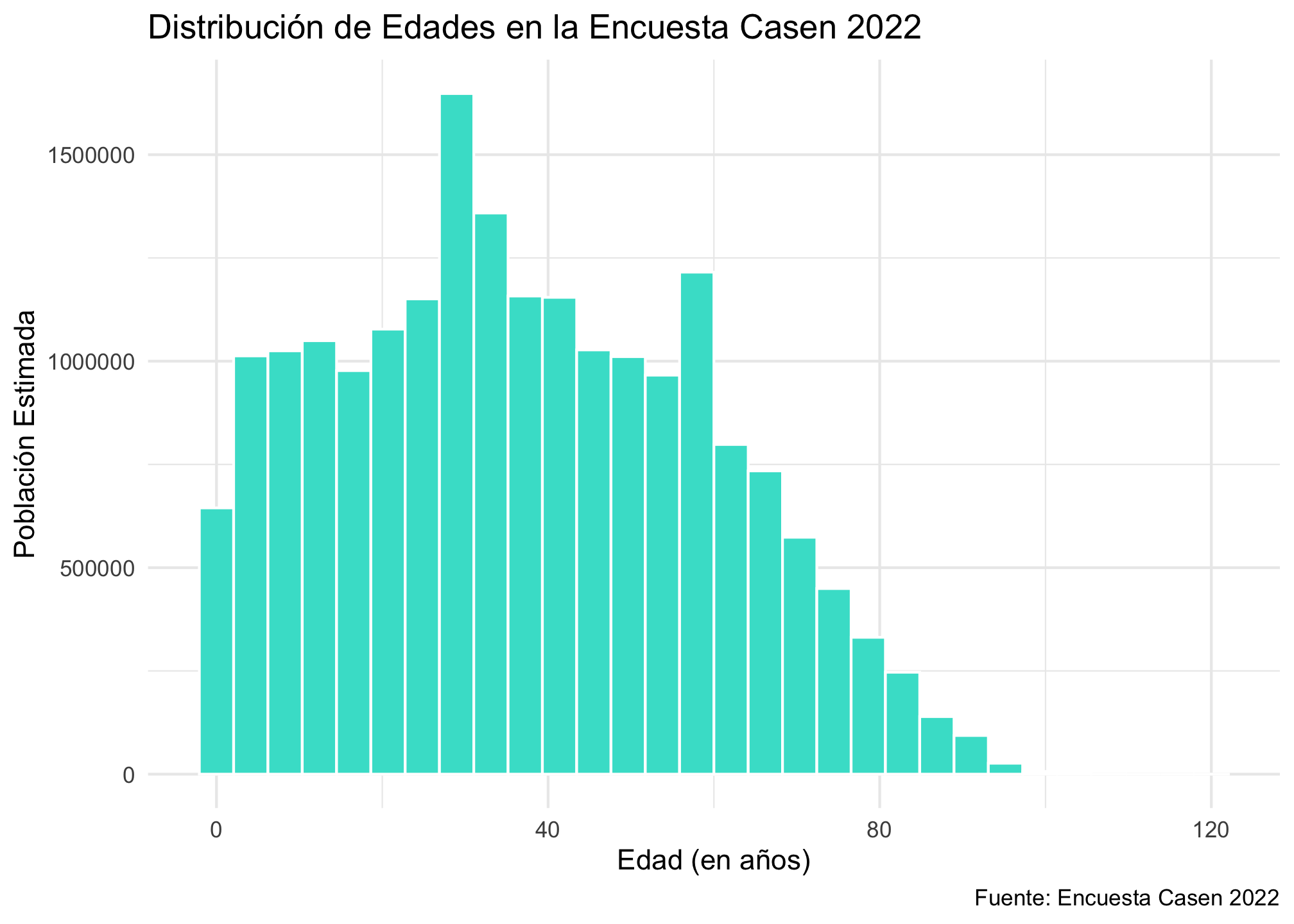
# Capa 4: Etiquetas y Título. Añadimos contexto con labs() y ponderador.
p_final <- ggplot(data = casen, mapping = aes(x = edad, weight = expr)) +
  geom_histogram(fill = "#40E0D0", color = "white", bins = 30) +
  labs(
    title = "Distribución de Edades en la Encuesta Casen 2022",
    x = "Edad (en años)",
    y = "Población Estimada",
    caption = "Fuente: Encuesta Casen 2022"
  ) +
  theme_minimal()

p_final

4. Gráficos para variables categóricas: geom_bar

En esta sección graficamos frecuencias absolutas y frecuencias relativas (porcentajes del total) para la variable pobreza, aplicando los ponderadores.

4.1 Preparación de la variable

Creamos una versión factorial legible de pobreza para etiquetas claras en el eje X.

casen <- casen %>%
  mutate(pobreza_factor = as_factor(pobreza))

4.2 Frecuencias absolutas (ponderadas)

Usamos weight = expr para que las alturas representen población expandida.

casen %>% 
  filter(!is.na(pobreza_factor)) %>%
  ggplot(aes(x = pobreza_factor, weight = expr)) +
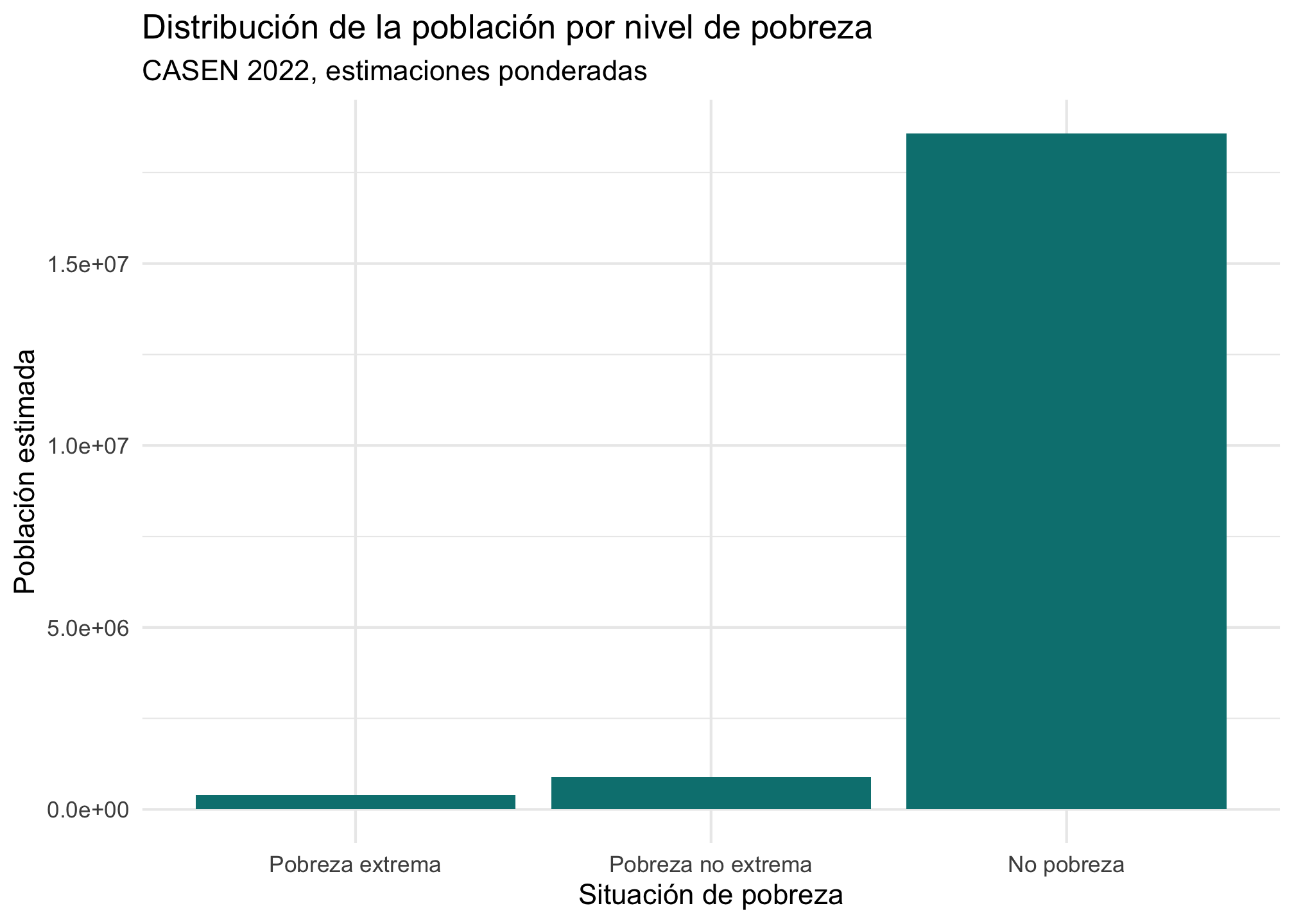
  geom_bar(fill = "#008080") +
  labs(
    title = "Distribución de la población por nivel de pobreza",
    subtitle = "CASEN 2022, estimaciones ponderadas",
    x = "Situación de pobreza",
    y = "Población estimada"
  ) +
  theme_minimal()

4.3 Frecuencias relativas (porcentajes del total, ponderadas)

Para porcentajes del total del gráfico, definimos y = after_stat(count / sum(count)) y formateamos el eje Y como porcentaje.

casen %>% 
  filter(!is.na(pobreza_factor)) %>%
  ggplot(aes(x = pobreza_factor, weight = expr)) +
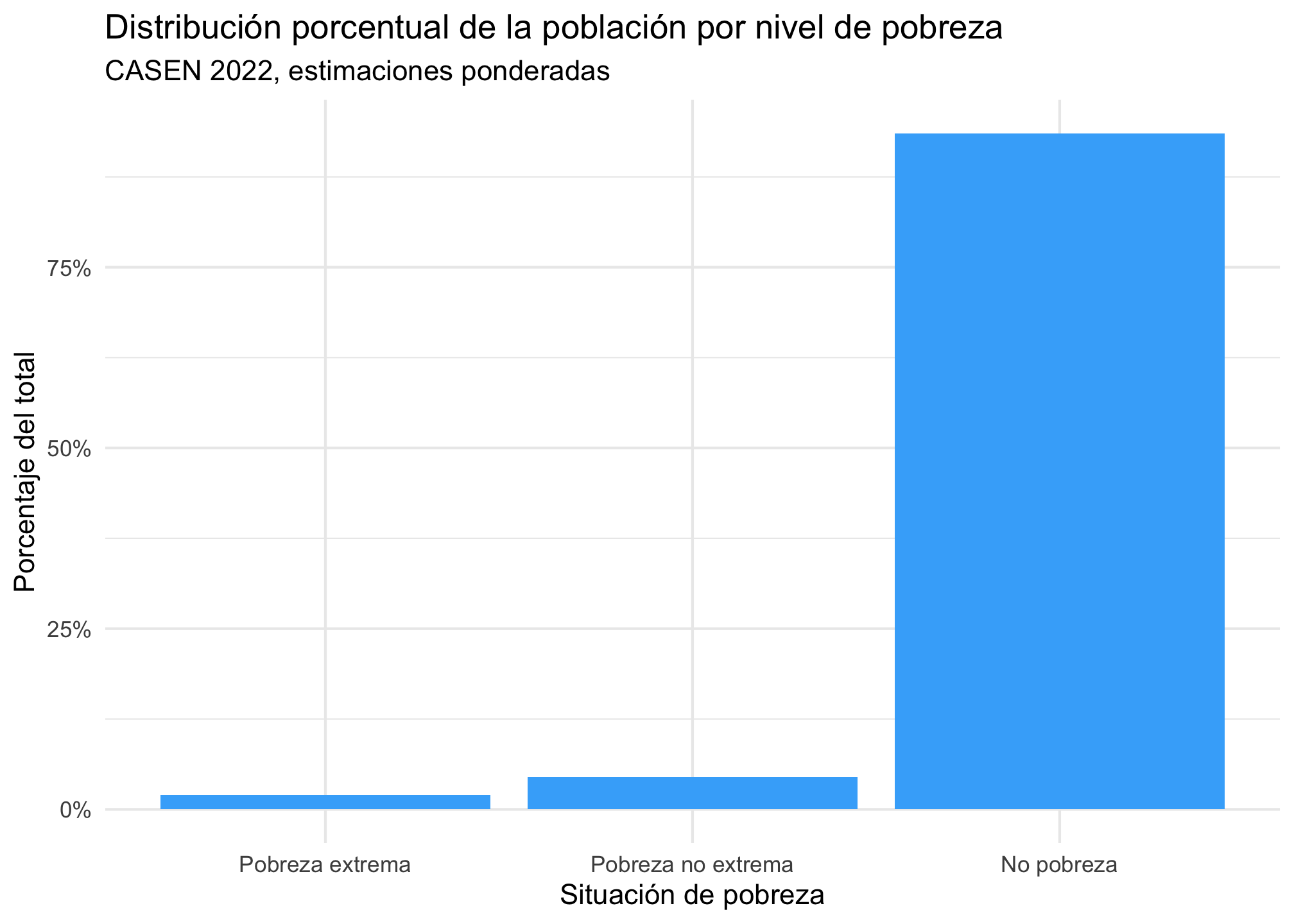
  geom_bar(aes(y = after_stat(count / sum(count))), fill = "#42affa") +
  scale_y_continuous(labels = scales::percent) +
  labs(
    title = "Distribución porcentual de la población por nivel de pobreza",
    subtitle = "CASEN 2022, estimaciones ponderadas",
    x = "Situación de pobreza",
    y = "Porcentaje del total"
  ) +
  theme_minimal()

Perfecto. Agrego la sección 4.4 con estructura docente y lista para usar.

4.4 Etiquetas sobre las barras

Usamos geom_text() para añadir etiquetas. La idea clave es usar la misma estadística que define la altura de la barra también para la posición (y) y para el texto (label).

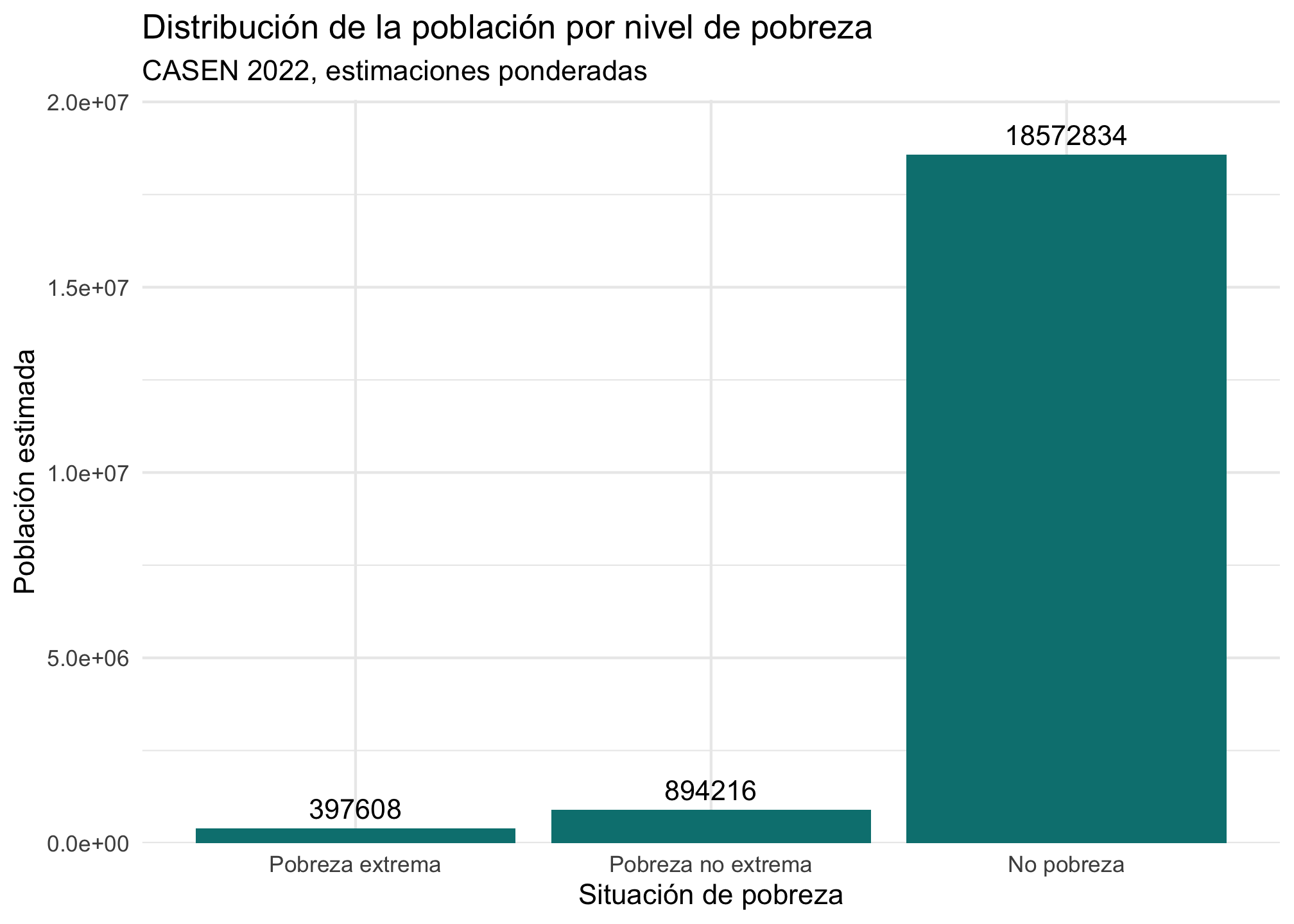
4.4.1 Frecuencias absolutas (ponderadas) con etiquetas

casen %>% 
  filter(!is.na(pobreza_factor)) %>%
  ggplot(aes(x = pobreza_factor, weight = expr)) +
  geom_bar(fill = "#008080") +
  geom_text(
    aes(
      y = after_stat(count),
      label = after_stat(sprintf("%.0f", count))
    ),
    stat = "count",
    vjust = -0.5,
    size = 3.8
  ) +
  scale_y_continuous(
    expand = expansion(mult = c(0, 0.08))  # pequeño margen superior para que entren las etiquetas
  ) +
  labs(
    title = "Distribución de la población por nivel de pobreza",
    subtitle = "CASEN 2022, estimaciones ponderadas",
    x = "Situación de pobreza",
    y = "Población estimada"
  ) +
  theme_minimal()

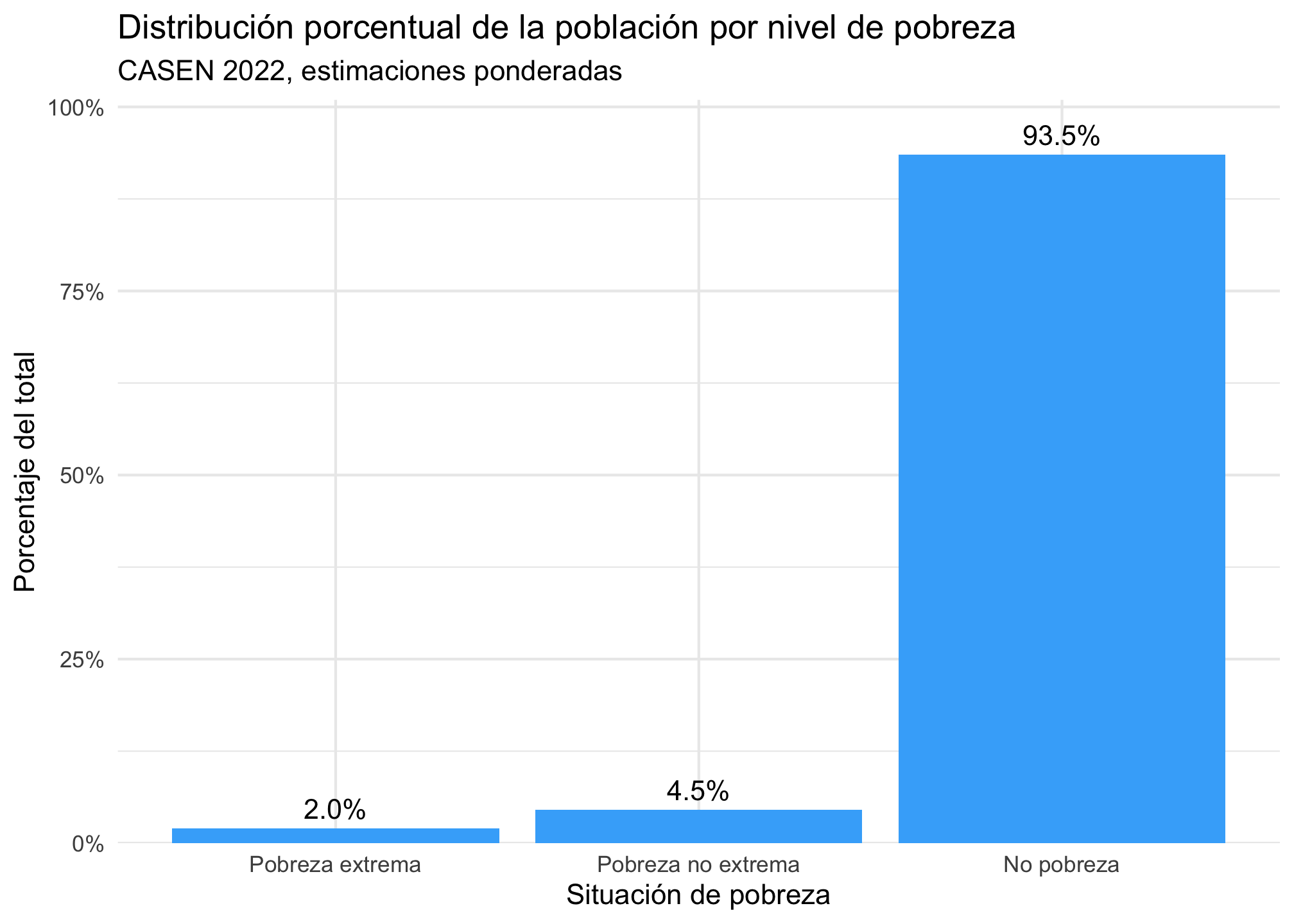
4.4.2 Porcentajes del total (ponderados) con etiquetas

casen %>% 
  filter(!is.na(pobreza_factor)) %>%
  ggplot(aes(x = pobreza_factor, weight = expr)) +
  geom_bar(aes(y = after_stat(count / sum(count))), fill = "#42affa") +
  geom_text(
    aes(
      y     = after_stat(count / sum(count)),
      label = after_stat(scales::percent(count / sum(count), accuracy = 0.1))
    ),
    stat = "count",
    vjust = -0.5,
    size  = 3.8
  ) +
  scale_y_continuous(
    labels = scales::percent,
    expand = expansion(mult = c(0, 0.08))
  ) +
  labs(
    title = "Distribución porcentual de la población por nivel de pobreza",
    subtitle = "CASEN 2022, estimaciones ponderadas",
    x = "Situación de pobreza",
    y = "Porcentaje del total"
  ) +
  theme_minimal()

5. La utilidad del Faceting: facet_wrap()

El faceting nos permite crear una grilla de gráficos para comparar subgrupos. Vamos a visualizar la relación entre edad y pobreza, separando por zona urbana y rural.

# 1. Preparamos los datos: calculamos el porcentaje de pobreza para cada edad y zona
casen_pob_zona <- casen %>%
  mutate(
    es_pobre = ifelse(pobreza %in% c(1, 2), 1, 0),
    zona_factor = as_factor(area)
    ) %>%
  filter(edad < 90) %>%
  group_by(edad, zona_factor) %>%
  # Usamos weighted.mean para un cálculo ponderado correcto de la proporción
  summarize(porc_pobreza = weighted.mean(es_pobre, w = expr, na.rm = TRUE) * 100, .groups = 'drop')

# 2. Creamos el gráfico facetado
ggplot(casen_pob_zona, aes(x = edad, y = porc_pobreza)) +
  geom_line(color = "#D76D77", linewidth = 1) +
  labs(
    title = "Porcentaje de Pobreza por Edad, según Zona Geográfica",
    x = "Edad",
    y = "% de Personas en Situación de Pobreza",
    caption = "Fuente: Casen 2022"
  ) +
  theme_bw() +
  facet_wrap(~ zona_factor) # La variable que define los paneles

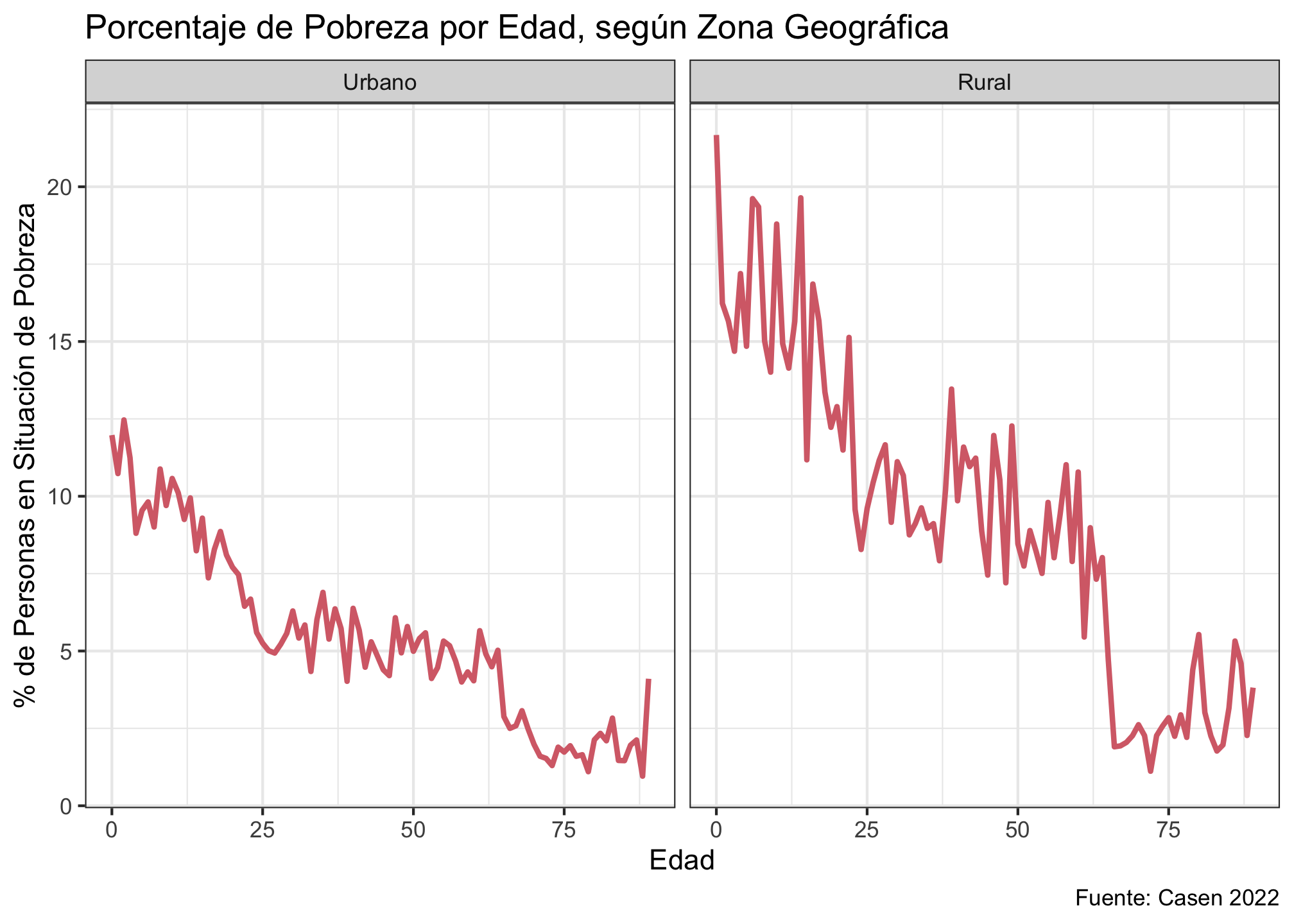Interpretación: El faceting revela un patrón claro: la tasa de pobreza es sistemáticamente más alta en la zona Rural que en la Urbana a lo largo de casi todo el ciclo de vida.

6. Actividad de Desafío

Tu misión es crear una sola figura (usando faceting) que compare la distribución del ingreso del trabajo (ytrabajocor) a través de las distintas categorías de pobreza (pobreza_factor).

Instrucciones:

  1. Filtra los datos para quedarte con ytrabajocor > 0 y ytrabajocor < 5000000 para una mejor visualización.
  2. Usa ggplot() y facet_wrap(~ pobreza_factor).
  3. Dentro de cada faceta, elige la geometría que mejor muestre la distribución del ingreso (geom_histogram o geom_density).
  4. Asegúrate de que tu gráfico sea ponderado (usa weight = expr).
  5. Aplica buenas prácticas: añade un título informativo, etiqueta los ejes y cita la fuente.
  6. Escribe un breve párrafo de interpretación: ¿Cómo cambia la distribución del ingreso (su centro, forma y dispersión) a medida que pasamos de “Pobreza Extrema” a “No Pobres”?
Previous
Next

Last updated on November 3, 2025