La Media, la Desviación Estándar y la Estandarización en R
0. Objetivos del Práctico
El objetivo de este práctico es aplicar las medidas de tendencia central y dispersión no robustas para describir variables cuantitativas y aprender a estandarizar sus valores. Al finalizar, serás capaz de:
- Calcular la media de forma “manual” y con la función
mean(). - Comparar la media y la mediana para diagnosticar la asimetría de una distribución.
- Calcular la varianza y la desviación estándar paso a paso para entender su lógica.
- Utilizar las funciones
var()ysd()para obtener estas medidas de forma eficiente. - Aplicar ponderadores (factores de expansión) para calcular estimaciones poblacionales.
- Calcular e interpretar puntuaciones Z para comparar observaciones de distintas distribuciones.
1. Contexto y Preparación de Datos
1.1 La Encuesta Suplementaria de Ingresos (ESI) 2024
Continuaremos trabajando con la ESI 2024. En este práctico, analizaremos dos variables cuantitativas clave:
ing_t_p: El ingreso del trabajo principal, una variable con fuerte asimetría positiva.efectivas: Las horas efectivas semanales trabajadas, una variable con una ligera asimetría negativa.
1.2 Carga de Paquetes y Datos
Paso 1: Organiza tu entorno de trabajo
- Asegúrate de estar trabajando dentro de tu Proyecto de RStudio.
- Dentro de tu proyecto, crea una carpeta llamada
datos.
Paso 2: Cargar paquetes Cargamos los paquetes que usaremos hoy.
# Cargar los paquetes que usaremos hoy
library(tidyverse)
library(haven)
library(DescTools)
library(Hmisc)
Paso 3: Cargar la base de datos El método recomendado es descargar el archivo y cargarlo desde tu proyecto. Puedes encontrar la base de datos en el siguiente enlace
# Paso 1: Descarga la base de datos desde el sitio del INE y guárdala
# en tu carpeta 'datos'. El archivo viene en formato .Rdata.
# Enlace: https://www.ine.gob.cl/docs/default-source/encuesta-suplementaria-de-ingresos/bbdd/rdata/2024/esi_2024.rdata
# Paso 2: Carga los datos usando la función load() y una ruta relativa
load("datos/esi_2024.rdata")
esi <- base # El objeto se llama 'base', lo renombramos a 'esi'
Para asegurar que este documento se pueda ejecutar de forma autocontenida, el siguiente código realiza la descarga y carga de forma automática. No necesitas ejecutarlo si ya cargaste la base manualmente.
# Código automático para cargar los datos desde la web
tmp <- tempfile(fileext = ".rdata")
download.file("https://www.ine.gob.cl/docs/default-source/encuesta-suplementaria-de-ingresos/bbdd/rdata/2024/esi_2024.rdata?sfvrsn=582b8630_4&download=true", tmp, mode = "wb")
load(tmp); esi <- base; unlink(tmp); rm(base, tmp)
Paso 4: Preparar la base de trabajo
Filtramos por la población de referencia (ocup_ref == 1) y limpiamos la variable de horas trabajadas, ya que los códigos 888 y 999 representan valores perdidos.
# Creamos nuestra base de trabajo filtrada y limpiamos la variable 'efectivas'
esi_trabajo <- esi %>%
filter(ocup_ref == 1) %>%
mutate(efectivas = ifelse(efectivas %in% c(888, 999), NA, efectivas))
2. La Media y el Diagnóstico de Asimetría
2.1 Media “Manual” vs. Función mean()
Para entender qué hace la media, podemos replicar su fórmula en R (suma / n). Lo haremos para la variable edad de la muestra.
# 1. Sumamos todos los valores
suma_edades <- sum(esi_trabajo$edad, na.rm = TRUE)
# 2. Contamos el número de casos validos
n_casos <- nrow(esi_trabajo %>% filter(!is.na(edad)))
# 3. Dividimos
media_manual <- suma_edades / n_casos
media_manual
## [1] 45.18962
# Ahora, con la función de R (da el mismo resultado)
mean(esi_trabajo$edad, na.rm = TRUE)
## [1] 45.18962
2.2 Media vs. Mediana: Diagnóstico de Asimetría en la Muestra
Comparemos la media y la mediana para ing_t_p y efectivas para ver qué nos dicen sobre la forma de la distribución en nuestra muestra.
esi_trabajo %>%
summarise(
media_horas = mean(efectivas, na.rm = TRUE),
mediana_horas = median(efectivas, na.rm = TRUE),
media_ingreso = mean(ing_t_p, na.rm = TRUE),
mediana_ingreso = median(ing_t_p, na.rm = TRUE)
)
## # A tibble: 1 × 4
## media_horas mediana_horas media_ingreso mediana_ingreso
## <dbl> <dbl> <dbl> <dbl>
## 1 37.0 44 758430. 560000
Interpretación:
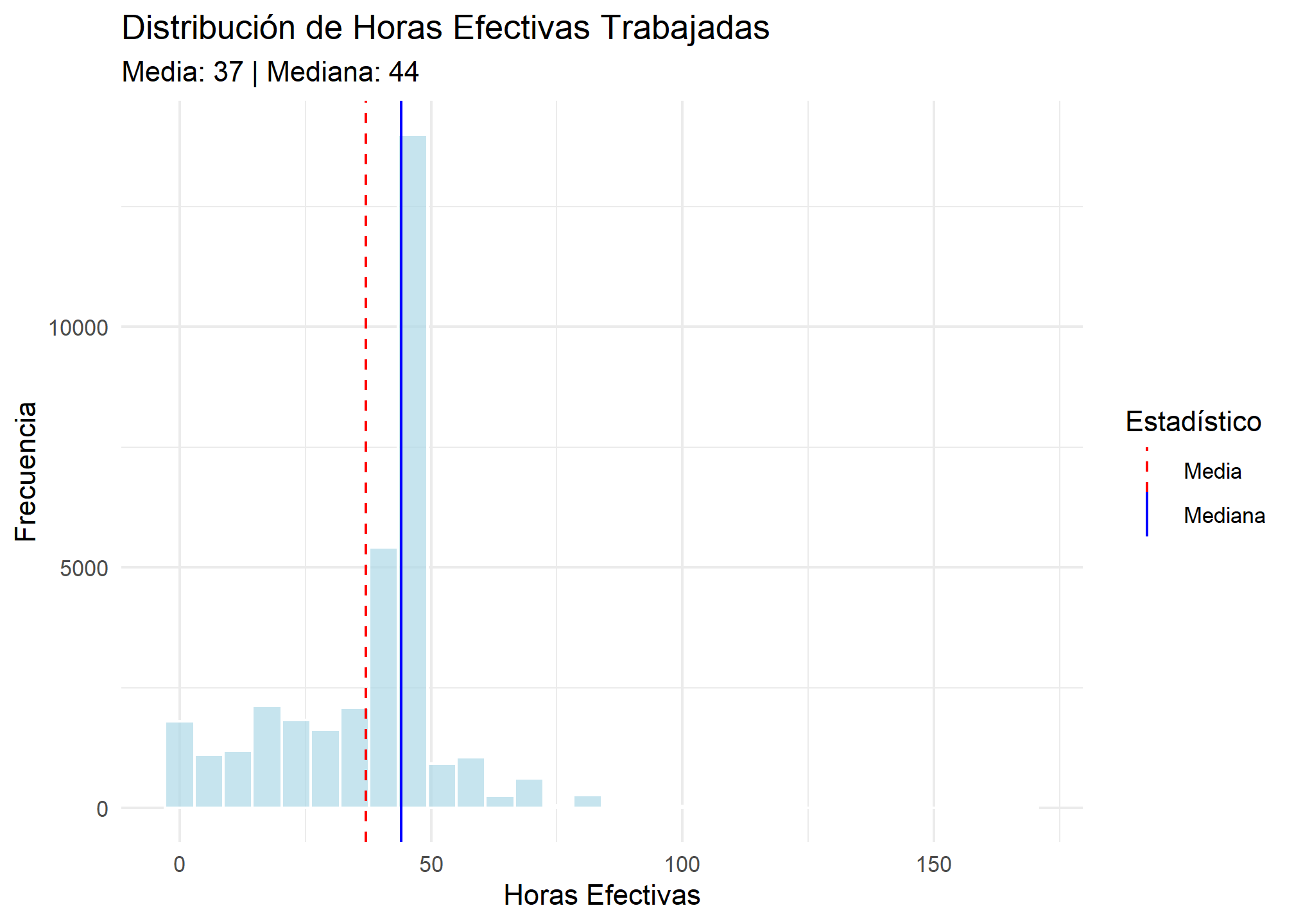
- Horas trabajadas: La media (37) es menor que la mediana (44), sugiriendo una asimetría a la izquierda.
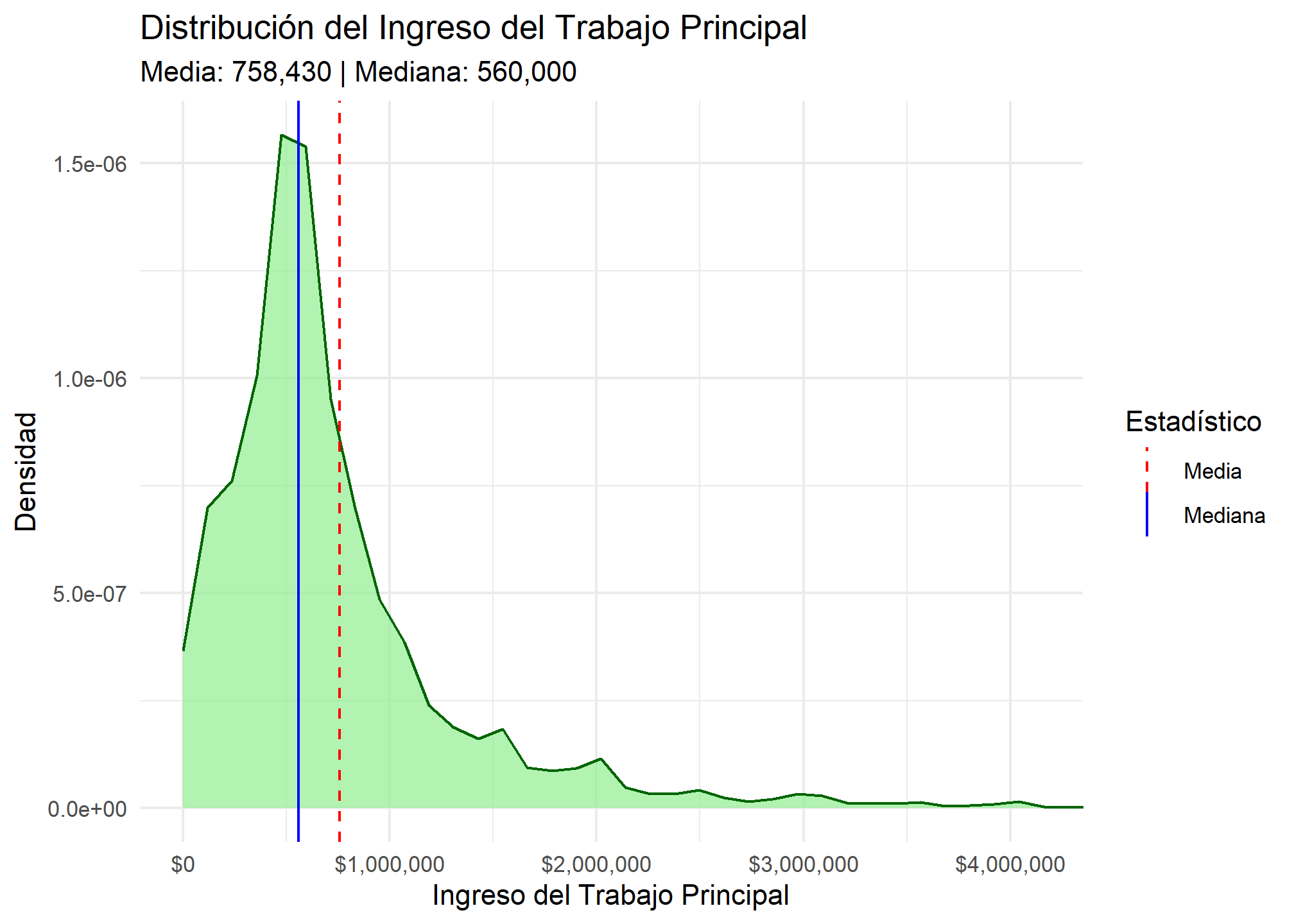
- Ingreso: La media (758,430) es mucho mayor que la mediana (560,000), una señal clara de asimetría a la derecha.
# Plot para 'efectivas' (horas trabajadas)
mean_efectivas <- mean(esi_trabajo$efectivas, na.rm = TRUE)
median_efectivas <- median(esi_trabajo$efectivas, na.rm = TRUE)
ggplot(esi_trabajo, aes(x = efectivas)) +
geom_histogram(fill = "lightblue", color = "white", alpha = 0.7) +
geom_vline(aes(xintercept = mean_efectivas, color = "Media"), linetype = "dashed") +
geom_vline(aes(xintercept = median_efectivas, color = "Mediana"), linetype = "solid") +
scale_color_manual(name = "Estadístico", values = c("Media" = "red", "Mediana" = "blue")) +
labs(
title = "Distribución de Horas Efectivas Trabajadas",
subtitle = paste0(
"Media: ", round(mean_efectivas, 1),
" | Mediana: ", round(median_efectivas, 1)
),
x = "Horas Efectivas",
y = "Frecuencia"
) +
theme_minimal()
# Plot para 'ing_t_p' (ingreso del trabajo principal)
mean_ing_t_p <- mean(esi_trabajo$ing_t_p, na.rm = TRUE)
median_ing_t_p <- median(esi_trabajo$ing_t_p, na.rm = TRUE)
ggplot(esi_trabajo, aes(x = ing_t_p)) +
geom_density(fill = "lightgreen", color = "darkgreen", alpha = 0.7) +
geom_vline(aes(xintercept = mean_ing_t_p, color = "Media"), linetype = "dashed") +
geom_vline(aes(xintercept = median_ing_t_p, color = "Mediana"), linetype = "solid") +
scale_color_manual(name = "Estadístico", values = c("Media" = "red", "Mediana" = "blue")) +
scale_x_continuous(labels = scales::label_dollar(prefix = "$", big.mark = ",", decimal.mark = ".")) +
labs(
title = "Distribución del Ingreso del Trabajo Principal",
subtitle = paste0(
"Media: ", format(round(mean_ing_t_p), big.mark = ","),
" | Mediana: ", format(round(median_ing_t_p), big.mark = ",")
),
x = "Ingreso del Trabajo Principal",
y = "Densidad"
) +
theme_minimal() +
coord_cartesian(xlim = c(0, quantile(esi_trabajo$ing_t_p, 0.99, na.rm = TRUE) * 1.05)) # Ajusta el límite para visibilidad
3. Comprendiendo la Varianza y la Desviación Estándar
Vamos a calcular la desviación estándar “paso a paso” para entender su lógica, usando la variable efectivas (horas trabajadas) de la muestra.
# Paso 1: Calcular la media de la muestra
media_horas <- mean(esi_trabajo$efectivas, na.rm = TRUE)
# Paso 2: Calcular las desviaciones al cuadrado
# Usamos mutate para crear una nueva columna con el cálculo
esi_trabajo <- esi_trabajo %>%
mutate(desv_cuadrado_horas = (efectivas - media_horas)^2)
# Paso 3: Sumar las desviaciones al cuadrado (esto es la "suma de cuadrados")
suma_cuadrados <- sum(esi_trabajo$desv_cuadrado_horas, na.rm = TRUE)
# Paso 4: Calcular la Varianza (dividiendo por n-1)
n <- sum(!is.na(esi_trabajo$efectivas)) # n de casos válidos
varianza_manual <- suma_cuadrados / (n - 1)
varianza_manual
## [1] 269.5194
# Paso 5: Calcular la Desviación Estándar (raíz cuadrada de la varianza)
sd_manual <- sqrt(varianza_manual)
sd_manual
## [1] 16.41705
# Comparemos con las funciones directas de R:
var(esi_trabajo$efectivas, na.rm = TRUE)
## [1] 269.5194
sd(esi_trabajo$efectivas, na.rm = TRUE)
## [1] 16.41705
Los resultados son idénticos. Ahora sabemos exactamente qué hacen las funciones var() y sd() por dentro.
4. Estimaciones Poblacionales Ponderadas
Para hacer afirmaciones sobre la población de Chile, debemos usar los ponderadores (fact_cal_esi).
# Usamos summarise() para calcular todas nuestras estimaciones poblacionales de una vez
resumen_poblacional <- esi_trabajo %>%
summarise(
media_ing_pob = weighted.mean(ing_t_p, w = fact_cal_esi, na.rm = TRUE),
sd_ing_pob = sqrt(wtd.var(ing_t_p, weights = fact_cal_esi, na.rm = TRUE)),
media_horas_pob = weighted.mean(efectivas, w = fact_cal_esi, na.rm = TRUE),
sd_horas_pob = sqrt(wtd.var(efectivas, weights = fact_cal_esi, na.rm = TRUE))
)
resumen_poblacional
## # A tibble: 1 × 4
## media_ing_pob sd_ing_pob media_horas_pob sd_horas_pob
## <dbl> <dbl> <dbl> <dbl>
## 1 897019. 1043897. 37.8 15.8
Interpretación:
- Se estima que el ingreso promedio del trabajo principal en Chile es de 897,019, con una desviación estándar de 1,043,897.
- Se estima que las horas efectivas trabajadas promedian 37.8 horas semanales, con una desviación estándar de 15.8 horas.
5. Cuantificando la Forma: Asimetría y Curtosis
Podemos confirmar numéricamente la forma de nuestras distribuciones poblacionales.
esi_trabajo %>%
summarise(
asimetria_ing = Skew(ing_t_p, weights = fact_cal_esi, na.rm = TRUE),
curtosis_ing = Kurt(ing_t_p, weights = fact_cal_esi, na.rm = TRUE),
asimetria_horas = Skew(efectivas, weights = fact_cal_esi, na.rm = TRUE),
curtosis_horas = Kurt(efectivas, weights = fact_cal_esi, na.rm = TRUE)
)
## # A tibble: 1 × 4
## asimetria_ing curtosis_ing asimetria_horas curtosis_horas
## <dbl> <dbl> <dbl> <dbl>
## 1 15.0 703. -0.473 1.72
Interpretación:
- Ingreso: La asimetría es extremadamente alta y positiva (14.98), y la curtosis también (702.66), indicando una distribución muy propensa a outliers.
- Horas: La asimetría es negativa (-0.47), confirmando la asimetría a la izquierda.
6. Puntuaciones Z: Estandarizando Nuestros Datos
6.1 Cálculo “Manual” y con la Función scale()
Vamos a crear una nueva columna con la puntuación Z para la variable edad.
# Primero, calculamos y guardamos la media y SD poblacionales de la edad
media_edad_pob <- weighted.mean(esi_trabajo$edad, w = esi_trabajo$fact_cal_esi, na.rm = TRUE)
sd_edad_pob <- sqrt(wtd.var(esi_trabajo$edad, weights = esi_trabajo$fact_cal_esi, na.rm = TRUE))
# Ahora usamos mutate para calcular la Z-score "manualmente" (método correcto)
esi_con_z <- esi_trabajo %>%
mutate(
z_edad_ponderado = (edad - media_edad_pob) / sd_edad_pob
)
# R base tiene la función scale() que hace esto, pero ¡cuidado! no es ponderada.
# La usamos solo para ver que la lógica es la misma y comparar.
esi_con_z <- esi_con_z %>%
mutate(z_edad_simple = as.numeric(scale(edad)))
# Comparamos las nuevas columnas
esi_con_z %>%
select(edad, z_edad_ponderado, z_edad_simple) %>%
head()
## # A tibble: 6 × 3
## edad z_edad_ponderado z_edad_simple
## <dbl> <dbl> <dbl>
## 1 54 0.827 0.626
## 2 22 -1.58 -1.65
## 3 63 1.50 1.27
## 4 45 0.148 -0.0135
## 5 29 -1.06 -1.15
## 6 49 0.450 0.271
Como vemos, los valores son muy similares, pero el cálculo manual con los estadísticos ponderados (z_edad_ponderado) es el correcto para interpretar la posición relativa a la población.
6.2 Interpretando las Puntuaciones Z
Las puntuaciones Z nos permiten encontrar los casos más “atípicos” o “extremos”.
# ¿Quién es la persona ocupada más joven en términos relativos?
esi_con_z %>%
arrange(z_edad_ponderado) %>% # Ordenamos de menor a mayor Z
select(edad, z_edad_ponderado) %>%
head(1)
## # A tibble: 1 × 2
## edad z_edad_ponderado
## <dbl> <dbl>
## 1 15 -2.11
Interpretación: La persona ocupada más joven en la muestra tiene 15 años. Su puntuación Z de -2.11 significa que su edad está casi 2.1 desviaciones estándar por debajo de la edad promedio de la población ocupada.
7. Actividad de Desafío
Ahora te toca a ti. Usando la base esi_trabajo:
- Cálculo de Estadísticos: Calcula la media, mediana, desviación estándar, asimetría y curtosis ponderadas para la variable
ing_t_p(ingreso del trabajo principal). - Diagnóstico: Escribe un párrafo de texto interpretando estos estadísticos. ¿Qué te dicen sobre el “ingreso típico” y sobre la forma de la distribución del ingreso en Chile?
- Cálculo de Puntuación Z: Calcula la puntuación Z para la variable
ing_t_pusando los estadísticos ponderados. - Análisis de Caso: Encuentra a una persona en la muestra cuyo ingreso sea lo más cercano posible al promedio (es decir, cuya puntuación Z sea la más cercana a 0 en valor absoluto). ¿Cuál es su ingreso y su puntuación Z? Pista: usa
mutate()para crear una Z absoluta (abs(z_ingreso)) y luegoarrange()sobre esa nueva variable.
# 1. Código para calcular los 5 estadísticos
# 2. Párrafo de interpretación (escríbelo como comentario en R)
# 3. Código para calcular la Z-score del ingreso
# 4. Código para encontrar a la persona "promedio"