Visualizando Distribuciones y Medidas Robustas: Histogramas y Boxplots en R

0. Objetivos del Práctico

El objetivo de este práctico es aplicar las herramientas de análisis exploratorio de datos (EDA) para describir la distribución de variables cuantitativas. Al finalizar, serás capaz de:

Crear e interpretar histogramas con R base y ggplot2 para analizar la forma de una distribución.
Calcular e interpretar medidas de centro y dispersión robustas (Mediana, Cuartiles, IQR) utilizando funciones base de R y dplyr.
Entender la necesidad de usar ponderadores (factores de expansión) para obtener estimaciones poblacionales precisas.
Construir e interpretar boxplots (geom_boxplot) como una poderosa herramienta visual para resumir y explorar datos.
Guardar los gráficos creados en archivos de imagen con ggsave().

1. Contexto y Preparación de Datos

1.1 La Encuesta Suplementaria de Ingresos (ESI)

En este práctico, trabajaremos con la Encuesta Suplementaria de Ingresos (ESI) del INE, correspondiente al año 2024. Esta encuesta es un módulo especializado de la Encuesta Nacional de Empleo (ENE) y es la principal fuente de datos de Chile para caracterizar en detalle los ingresos laborales de las personas ocupadas. Sus resultados son fundamentales para analizar la desigualdad, la pobreza y la efectividad de las políticas públicas.

Nos centraremos en la variable ing_t_p (ingreso del trabajo principal), un ejemplo clásico de una variable cuantitativa con una distribución asimétrica.

1.2 Carga de Paquetes y Datos

Paso 1: Organiza tu entorno de trabajo

Antes de empezar, asegúrate de tener una buena organización.

Crea un Proyecto de RStudio para este curso o unidad si aún no lo tienes.
Dentro de tu proyecto, crea una carpeta llamada datos.

Paso 2: Cargar paquetes

Cargamos tidyverse, que incluye ggplot2 para los gráficos, y haven para leer los datos.

# Cargar los paquetes que usaremos hoy
library(tidyverse)
library(haven)
# Instala el paquete si no lo tienes: install.packages("DescTools")
library(DescTools)
library(knitr)
library(kableExtra)

Paso 3: Cargar la base de datos

Vamos a cargar la base de datos de la ESI. El método recomendado es descargar el archivo y cargarlo desde tu proyecto.

# Paso 1: Descarga la base de datos desde el sitio del INE y guárdala 
# en tu carpeta 'datos'. El archivo viene en formato .Rdata.
# Enlace: https://www.ine.gob.cl/docs/default-source/encuesta-suplementaria-de-ingresos/bbdd/rdata/2024/esi_2024.rdata

# Paso 2: Carga los datos usando la función load() y una ruta relativa
load("datos/esi_2024.rdata")
esi <- base # El objeto dentro del .Rdata se llama 'base', lo renombramos a 'esi'

Nota sobre la reproducibilidad: Para que este práctico funcione de manera autocontenida, a continuación se incluye un código que realiza la descarga y carga de forma automática. No necesitas ejecutarlo si ya cargaste la base manualmente.

# Código automático para cargar los datos desde la web
tmp <- tempfile(fileext = ".rdata")
download.file("https://www.ine.gob.cl/docs/default-source/encuesta-suplementaria-de-ingresos/bbdd/rdata/2024/esi_2024.rdata?sfvrsn=582b8630_4&download=true", tmp, mode = "wb")
load(tmp); esi <- base; unlink(tmp); rm(base, tmp)

Paso 4: Preparar la base de trabajo

Para nuestro análisis, nos enfocaremos en la población de referencia del estudio: personas ocupadas que tienen la misma ocupación que el mes pasado (ocup_ref == 1). Esto es importante para que los ingresos que declaran coincidan con la información de su ocupación.

# Creamos nuestra base de trabajo filtrada
esi_trabajo <- esi %>%
  filter(ocup_ref == 1)

2. Visualizando la Forma: Histogramas

2.1 Histograma con R Base: Un Vistazo Rápido

La función hist() de R base es excelente para una exploración inicial y rápida, pero ten en cuenta que no utiliza el ponderador.

hist(esi_trabajo$ing_t_p,
     main = "Histograma de Ingreso del Trabajo Principal (R Base)",
     xlab = "Ingreso Mensual ($ CLP)",
     ylab = "Frecuencia (conteo de la muestra)",
     col = "#D76D77",
     breaks = 100) # 'breaks' controla el número de barras

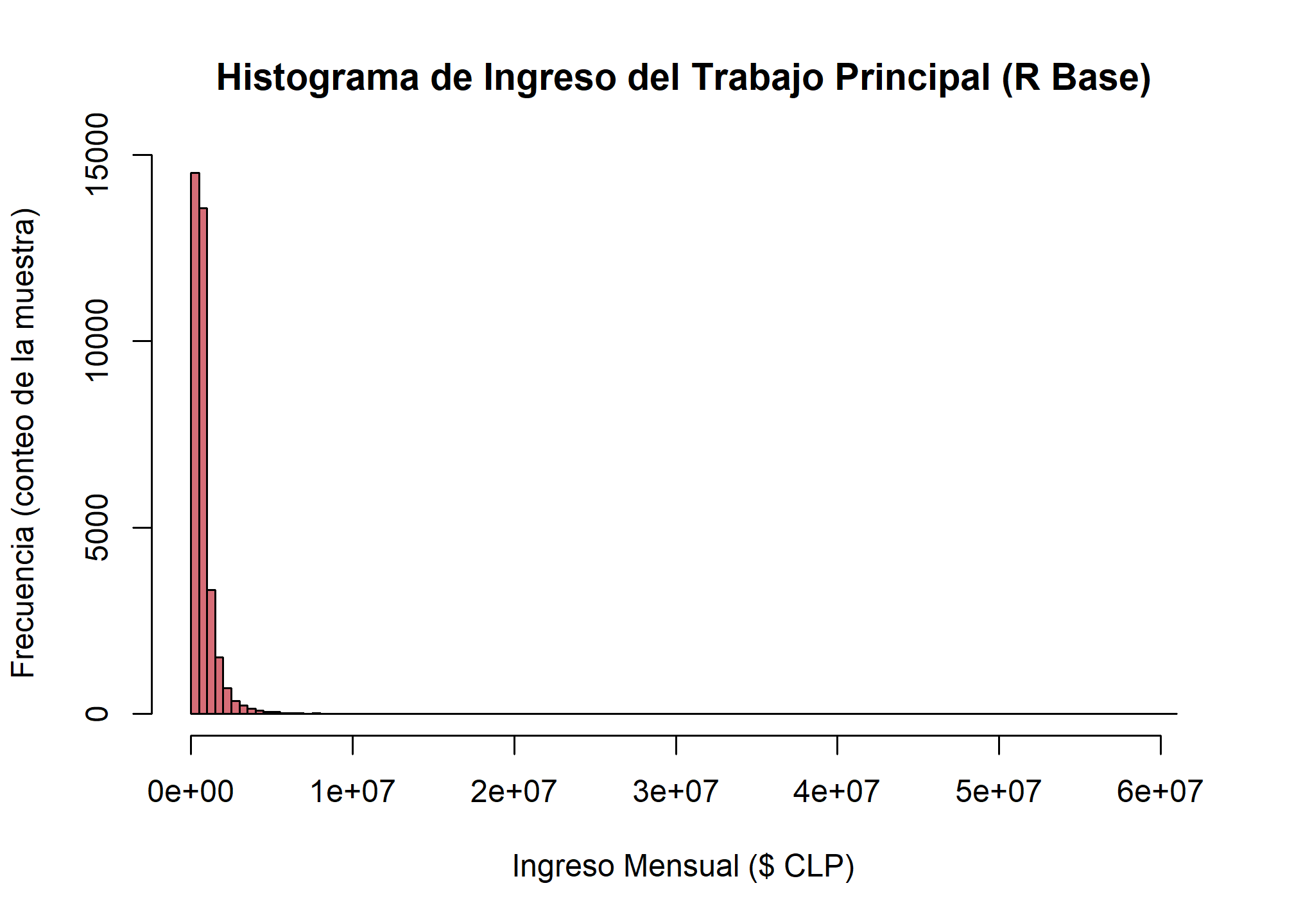
Interpretación: Vemos una distribución muy concentrada a la izquierda. La mayoría de los trabajadores en la muestra tiene ingresos bajos, pero la larga cola a la derecha indica la presencia de unos pocos con ingresos muy altos.

2.2 Histograma con `ggplot2`: Más Control y Estimación Poblacional

ggplot2 nos da un control más detallado y nos permite incorporar los factores de expansión en la estética (aes) del gráfico para obtener una estimación de la distribución en la población.

# Filtramos para ingresos menores a 5 millones para visualizar mejor la forma
esi_trabajo %>%
  filter(ing_t_p < 5000000) %>%
  ggplot(aes(x = ing_t_p, weight = fact_cal_esi)) +
  geom_histogram(binwidth = 100000, fill = "#D76D77", color = "white") +
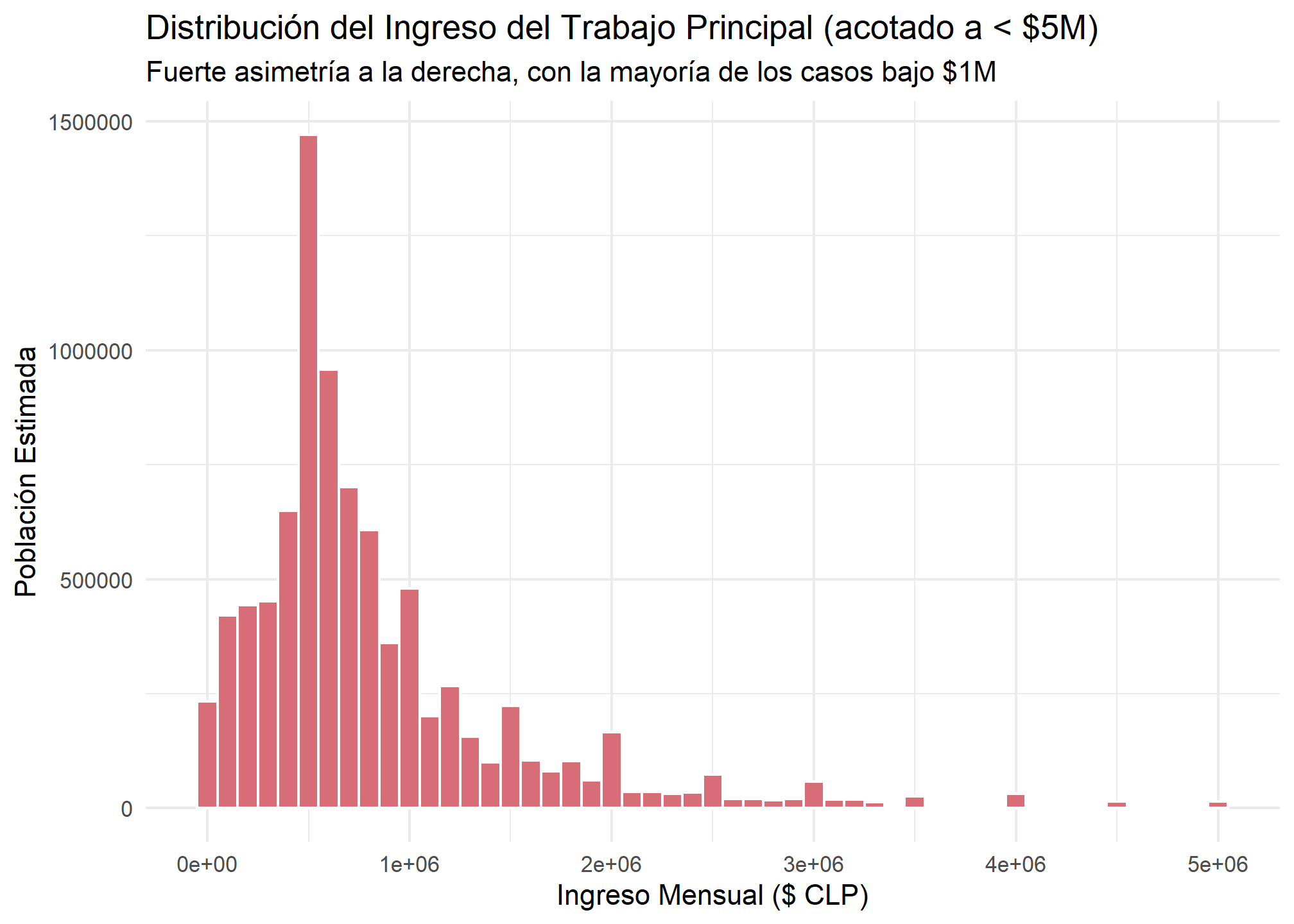
  labs(
    title = "Distribución del Ingreso del Trabajo Principal (acotado a < $5M)",
    subtitle = "Fuerte asimetría a la derecha, con la mayoría de los casos bajo $1M",
    x = "Ingreso Mensual ($ CLP)",
    y = "Población Estimada"
  ) +
  theme_minimal()

3. Cálculo de Medidas Robustas

3.1 Mediana y Cuantiles con Funciones Base (Sin Ponderar)

Antes de realizar cálculos poblacionales, es útil explorar la muestra. Las funciones median() y quantile() son perfectas para esto.

# Mediana de la muestra (sin ponderar)
mediana_muestra <- median(esi_trabajo$ing_t_p, na.rm = TRUE)
mediana_muestra

## [1] 560000

Interpretación: El 50% de las personas en nuestra muestra gana $560.000 o menos.

# Cuantiles de la muestra (sin ponderar)
# La función quantile() nos permite pedir cualquier percentil usando el argumento 'probs'
quantile(esi_trabajo$ing_t_p, probs = c(0, 0.25, 0.5, 0.75, 1), na.rm = TRUE)

##         0%        25%        50%        75%       100% 
##        0.0   400000.0   560000.0   888579.9 60756649.4

Interpretación: El 25% de la muestra gana $400.000 o menos (Q1), mientras que el 75% gana $888.580 o menos (Q3). Esto nos da una idea de la dispersión del 50% central de los datos en la muestra.

3.2 Agregando Medidas con `summarise()`

Podemos calcular múltiples estadísticos a la vez usando summarise() de dplyr, lo que es mucho más eficiente.

esi_trabajo %>%
  summarise(
    mediana = median(ing_t_p, na.rm = TRUE),
    q1 = quantile(ing_t_p, probs = 0.25, na.rm = TRUE),
    q3 = quantile(ing_t_p, probs = 0.75, na.rm = TRUE),
    iqr = IQR(ing_t_p, na.rm = TRUE)
  )

## # A tibble: 1 × 4
##   mediana     q1      q3     iqr
##     <dbl>  <dbl>   <dbl>   <dbl>
## 1  560000 400000 888580. 488580.

3.3 Incorporando Factores de Expansión

Los cálculos anteriores describen la muestra. Para describir a la población, debemos usar ponderadores. El paquete DescTools tiene funciones que lo permiten, y podemos integrarlas dentro de nuestro flujo de dplyr.

# Calculamos la mediana y cuantiles ponderados usando summarise()
esi_trabajo %>%
  summarise(
    mediana_pob = Median(ing_t_p, weights = fact_cal_esi, na.rm = TRUE),
    q1_pob = Quantile(ing_t_p, weights = fact_cal_esi, probs = 0.25, na.rm = TRUE),
    q3_pob = Quantile(ing_t_p, weights = fact_cal_esi, probs = 0.75, na.rm = TRUE)
  )

## # A tibble: 1 × 3
##   mediana_pob  q1_pob   q3_pob
##         <dbl>   <dbl>    <dbl>
## 1      611000 451725. 1003420.

Interpretación: Ahora sí podemos afirmar que se estima que el 50% de la población ocupada en Chile gana $611.000 o menos. Además, el 25% más bajo gana $451.725 o menos, y el 75% gana $1.003.420 o menos. Estos valores son distintos a los de la muestra, lo que demuestra la importancia de usar siempre el factor de expansión para realizar inferencias.

Para presentar estos resultados de manera más formal y clara en nuestro informe, podemos usar la función kable() del paquete knitr, junto con kable_styling() del paquete kableExtra.

# Primero, guardamos el resultado de nuestro cálculo en un objeto
tabla_resumen_pob <- esi_trabajo %>%
  summarise(
    `Primer Cuartil (Q1)` = Quantile(ing_t_p, weights = fact_cal_esi, probs = 0.25, na.rm = TRUE),
    `Mediana` = Median(ing_t_p, weights = fact_cal_esi, na.rm = TRUE),
    `Tercer Cuartil (Q3)` = Quantile(ing_t_p, weights = fact_cal_esi, probs = 0.75, na.rm = TRUE)
  )

# Ahora, creamos la tabla formateada
knitr::kable(
  tabla_resumen_pob,
  caption = "Estadísticos Robustos Ponderados para el Ingreso del Trabajo Principal ($ CLP)",
  digits = 0, # Sin decimales
  format.args = list(big.mark = ".") # Usamos punto como separador de miles
) %>%
  kable_styling(bootstrap_options = "striped", full_width = FALSE)

Table 1: (\#tab:unnamed-chunk-3)Estadísticos Robustos Ponderados para el Ingreso del Trabajo Principal ($ CLP)
Primer Cuartil (Q1)	Mediana	Tercer Cuartil (Q3)
451.725	611.000	1.003.420

4. Visualizando con Boxplots

4.1 Boxplot del Ingreso: El Problema de la Asimetría

esi_trabajo %>%
  ggplot(aes(x = "", y = ing_t_p, weight = fact_cal_esi )) + # Eje X vacío para un solo boxplot
  geom_boxplot(fill = "#3A1C71", outlier.alpha = 0.1) +
  labs(
    title = "Boxplot del Ingreso del Trabajo Principal (Muestra sin ponderar)",
    y = "Ingreso Mensual ($ CLP)",
    x = ""
  ) +
  theme_minimal()

Interpretación: El gráfico es casi inútil. La caja está completamente aplastada en la parte inferior y una nube masiva de outliers domina la visualización. Esto es una señal visual muy potente de la extrema asimetría de la variable.

4.2 La Solución: Escala Logarítmica

Para solucionarlo, usamos una escala logarítmica en el eje Y para “comprimir” los valores altos y poder ver la caja.

# Creamos el boxplot con escala logarítmica y lo guardamos en un objeto
boxplot_log <- esi_trabajo %>%
  ggplot(aes(x = "", y = ing_t_p, weight = fact_cal_esi)) +
  geom_boxplot(fill = "#3A1C71", outlier.alpha = 0.1) +
  scale_y_log10(labels = scales::dollar_format(prefix = "$", big.mark = ".")) +
  labs(
    title = "Boxplot del Ingreso (Eje Y Logarítmico)",
    subtitle = "Visualización de la muestra sin ponderar",
    y = "Ingreso Mensual ($ CLP, escala log)",
    x = ""
  ) +
  theme_minimal()

# Mostramos el gráfico
boxplot_log

Interpretación: Ahora la caja es visible. Podemos apreciar la posición de la mediana, el rango intercuartil (el tamaño de la caja) y la extensión de los bigotes, dándonos una visión completa y robusta de la distribución del ingreso en la muestra.

5. Guardando tus Gráficos con `ggsave()`

Una vez que tienes un gráfico de ggplot2 que te gusta, puedes guardarlo como un archivo de imagen de alta calidad con ggsave().

# La función ggsave() guarda el último gráfico que mostraste por defecto.
# Es buena práctica guardarlo en una carpeta separada, por ejemplo, 'output' o 'graficos'.

# Primero, asegúrate de crear la carpeta 'graficos' en tu proyecto.
dir.create("graficos")

ggsave("graficos/boxplot_ingreso_log.png", 
       plot = boxplot_log, # Es buena práctica especificar qué gráfico guardar
       width = 8,         # Ancho en pulgadas
       height = 6,        # Alto en pulgadas
       dpi = 300)         # Resolución (puntos por pulgada), 300 es ideal para publicación

6. Actividad de Desafío

Usando la base de datos esi_trabajo y las herramientas que aprendimos hoy, realiza el siguiente análisis sobre la variable efectivas (“Horas efectivas semanales trabajadas”):

Primero, debes limpiar la variable: los valores 888 y 999 son códigos para casos perdidos y deben ser reemplazados por NA.
Crea un histograma ponderado de efectivas usando ggplot2. Describe su forma (¿es simétrica, asimétrica, unimodal, bimodal?). Presta especial atención a los picos más prominentes.
Calcula la mediana ponderada y los cuartiles ponderados (Q1 y Q3) para la misma variable. Interpreta el valor de la mediana en una frase completa (ej. “Se estima que el 50% de la población ocupada trabajó…").
Crea un boxplot de efectivas. ¿Qué te dice este gráfico sobre la distribución que complementa (o confirma) lo que viste en el histograma?
Guarda tu histograma en un archivo llamado "histograma_horas.png" dentro de tu carpeta graficos.

# 1. Limpiar casos perdidos
esi_trabajo <- esi_trabajo %>% 
  mutate(efectivas = ifelse(efectivas %in% c(888, 999), NA, efectivas))


# 2. Código para el histograma


# 3. Código para el cálculo de mediana y cuartiles ponderados


# 4. Código para el boxplot


# 5. Código para guardar el gráfico

Last updated on October 25, 2025